Giải SBT Toán 7 trang 57 Tập 1 Kết nối tri thức
Haylamdo sưu tầm và biên soạn Giải SBT Toán 7 trang 57 Tập 1 trong Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác Sách bài tập Toán lớp 7 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 57.
Giải SBT Toán 7 trang 57 Tập 1 Kết nối tri thức
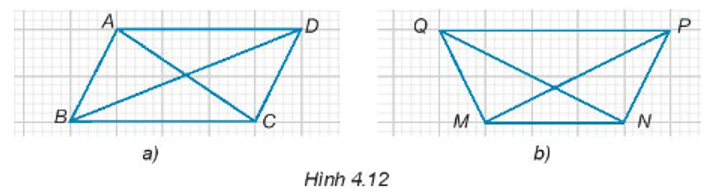
Bài 4.13 trang 57 sách bài tập Toán lớp 7 Tập 1: Trong mỗi hình vẽ trên lưới ô vuông dưới đây, hãy chỉ ra một cặp hai tam giác bằng nhau.
Lời giải:
*) Ở Hình 4.12a) ta thấy: ∆ABC = ∆CDA vì:
AB = DC (đều bằng đường chéo hình chữ nhật được tạo thành từ hai ô vuông nhỏ)
AC: cạnh chung
BC = AD (bằng độ dài 4 ô vuông nhỏ xếp liền nhau)
Do đó, ∆ABC = ∆CDA (c – c – c).
*) Ở Hình 4.12b) ta thấy: ∆MQN = ∆NPM vì:
MQ = NP (đều bằng đường chéo hình chữ nhật được tạo thành từ hai ô vuông nhỏ)
MN: cạnh chung
PM = NQ (đều bằng độ dài đường chéo hình chữ nhật có chiều dài là 4 ô vuông xếp liền nhau và chiều rộng là hai ô vuông xếp liền nhau).
Do đó, ∆MQN = ∆NPM (c – c – c) .
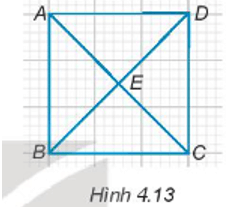
Bài 4.14 trang 57 sách bài tập Toán lớp 7 Tập 1: Cho Hình 4.13, ABCD là hình vuông. E là giao của AC và BD. Hãy chỉ ra các cặp tam giác bằng nhau có chung đỉnh E.
Lời giải:
Ta có: AB = BC = CD = DA (đều bằng 3 ô vuông) và EA = EB = EC = ED.
Vậy theo trường hợp bằng nhau cạnh – cạnh – cạnh, ta có các cặp tam giác bằng nhau có chung đỉnh E là:
∆EAD = ∆EDC; ∆EAD = ∆ECB; ∆EAD = ∆EBA;
∆EDC = ∆ECB; ∆EDC = ∆EDA; ∆ECB = ∆EBA;
∆EAD = ∆ECD; ∆EAD = ∆EBC; ∆EAD = ∆EAB;
∆EDC = ∆EBC; ∆EDC = ∆EDA; ∆ECB = ∆EAB.
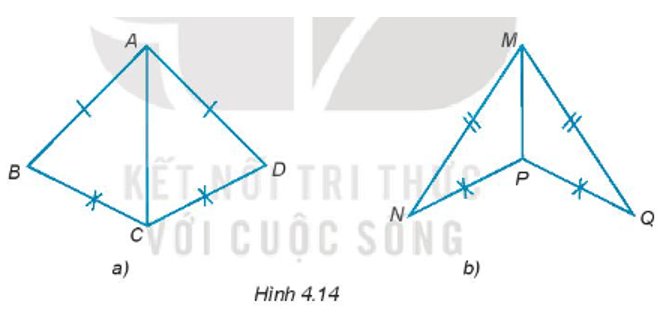
Bài 4.15 trang 57 sách bài tập Toán lớp 7 Tập 1: Cho Hình 4.14, chứng minh rằng ∆ABC = ∆ADC; ∆MNP = ∆MQP.
Lời giải:
a) Xét ∆ABC và ∆ADC có:
AB = AD (giả thiết)
BC = DC (giả thiết)
AC chung
Do đó, ∆ABC = ∆ADC (c – c – c).
b) Xét ∆MNP và ∆MQP có:
MP chung
NP = PQ (giả thiết)
MN = MQ (giả thiết)
Do đó, ∆MNP = ∆MQP (c – c – c).
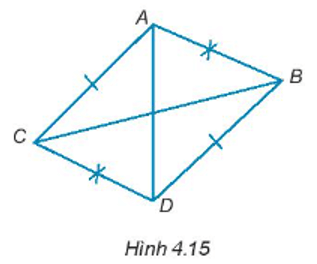
Bài 4.16 trang 57 sách bài tập Toán lớp 7 Tập 1: Cho Hình 4.15, chứng minh rằng ∆ABC = ∆DCB; ∆ADB = ∆DAC.
Lời giải:
Xét ∆ABC và ∆DCB có:
AB = DC (giả thiết)
AC = BD (giải thiết)
BC chung
Do đó, ∆ABC = ∆DCB (c – c – c).
Xét hai tam giác ∆ADB và ∆DAC có:
AB = DC (giả thiết)
BD = AC (giải thiết)
AD chung
Do đó, ∆ADB = ∆DAC (c – c – c).
Lời giải sách bài tập Toán lớp 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác Kết nối tri thức hay khác: