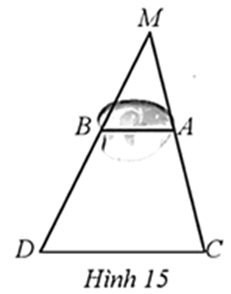
Trong công viên có một dẻo đất có dạng hình tam giác MCD được mô tả như Hình 15

Trong công viên có một dẻo đất có dạng hình tam giác MCD được mô tả như . Giữa hai điểm A, B là một hồ nước sâu và một con đường đi bộ giữa C và D. Bạn An đi từ C đến D với tốc độ 100 m/phút trong thời gian 2 phút 42 giây. Tính độ dài AB, biết AB // CD và

Giải SBT Toán 8 Bài 2: Ứng dụng của định lí Thalès trong tam giác - Cánh diều

Bài 10 trang 62 SBT Toán 8 Tập 2: Trong công viên có một dẻo đất có dạng hình tam giác MCD được mô tả như Hình 15. Giữa hai điểm A, B là một hồ nước sâu và một con đường đi bộ giữa C và D. Bạn An đi từ C đến D với tốc độ 100 m/phút trong thời gian 2 phút 42 giây. Tính độ dài AB, biết AB // CD và $MB=\frac{4}{5}BD.$

Lời giải:

Đổi 2 phút 42 giây = $\frac{27}{10}$ phút.

Khi đó độ dài CD là $CD=100\cdot \frac{27}{10}=270$ (m).

Do $MB=\frac{4}{5}BD$ nên $\frac{MB}{BD}=\frac{4}{5}$, do đó $\frac{MB}{BD+MB}=\frac{4}{5+4}$ hay $\frac{MB}{MD}=\frac{4}{9}$

Xét ∆MCD với AB // CD, ta có: $\frac{AB}{CD}=\frac{MB}{MD}=\frac{4}{9}$ (hệ quả của định lí Thalès)

Hay $AB=\frac{4}{9}CD.$

Vậy độ dài AB là: $AB=\frac{4}{9}\cdot 270=120$ (m).

Lời giải SBT Toán 8 Bài 2: Ứng dụng của định lí Thalès trong tam giác hay khác:

• Bài 11 trang 62 SBT Toán 8 Tập 2: Ở một nhà máy, người ta dùng một băng chuyền để chuyển nguyên vật liệu. Ba vòng quay A, B, C của băng chuyền đặt cách mặt đất ở ....

• Bài 12 trang 63 SBT Toán 8 Tập 2: Một con dốc có độ nghiêng 30° so với mặt đất bằng phẳng. Đỉnh con dốc có độ cao CA là 500 m (Hình 17) ....

• Bài 13 trang 63 SBT Toán 8 Tập 2: Một ngôi nhà có thiết kế mái như Hình 18 và có các số đo như sau: AD = 1,5 m, DE = 2,5 m, BF = CG = 1 m, FG = 5,5 m ....