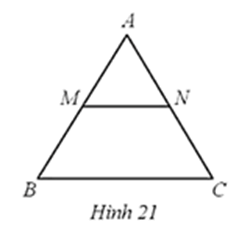
Hình 21 cho biết cạnh của tam giác đều ABC bằng 6 cm; M, N lần lượt là trung điểm
cho biết cạnh của tam giác đều ABC bằng 6 cm; M, N lần lượt là trung điểm các cạnh AB, AC. Chỉ ra phát biểu trong các phát biểu sau:
Giải SBT Toán 8 Bài 3: Đường trung bình của tam giác - Cánh diều
Bài 15 trang 65 SBT Toán 8 Tập 2: Hình 21 cho biết cạnh của tam giác đều ABC bằng 6 cm; M, N lần lượt là trung điểm các cạnh AB, AC. Chỉ ra phát biểu sai trong các phát biểu sau:
a) Tam giác AMN là tam giác đều.
b) Hình thang BMNC là hình thang cân.
c) Chu vi tứ giác BMNC bằng hai phần ba chu vi tam giác ABC.
d) Độ dài đường trung bình MN bằng 2 cm.
Lời giải:
• Do M, N lần lượt là trung điểm của AB, AC nên ;
Mà AB = AC và (do tam giác ABC đều)
Nên AM = AN và
Do đó tam giác AMN là tam giác đều. Do đó phát biểu a) là đúng.
⦁ Xét ∆ABC có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác nên MN // BC.
Xét tứ giác MNCB có MN // BC nên là hình thang
Lại có (do tam giác ABC đều) nên MNCB là hình thang cân.
Do đó phát biểu b) là đúng.
⦁ Do MN là đường trung bình của tam giác ABC nên (cm).
Do đó phát biểu d) là sai.
⦁ Chu vi tam giác ABC là: AB + BC + CA = 6 + 6 + 6 = 18 cm.
Do ; nên BM = NC = 3 cm.
Chu vi tứ giác BMNC là: BM + MN + NC + CB = 3 + 3 + 3 + 6 = 15 (cm).
Vậy tỉ số giữa chu vi tứ giác BMNC và chu vi tam giác ABC là
Do đó phát biểu c) là sai.
Vậy các phát biểu sai là: c), d).
Lời giải SBT Toán 8 Bài 3: Đường trung bình của tam giác hay khác: