Cho tứ giác ABCD có M, N lần lượt là trung điểm của AD, BC
Cho tứ giác ABCD có M, N lần lượt là trung điểm của AD, BC. Chứng minh: . Dấu đẳng thức xảy ra khi nào?
Giải SBT Toán 8 Bài 3: Đường trung bình của tam giác - Cánh diều
Bài 20* trang 66 SBT Toán 8 Tập 2: Cho tứ giác ABCD có M, N lần lượt là trung điểm của AD, BC. Chứng minh: . Dấu đẳng thức xảy ra khi nào?
Lời giải:
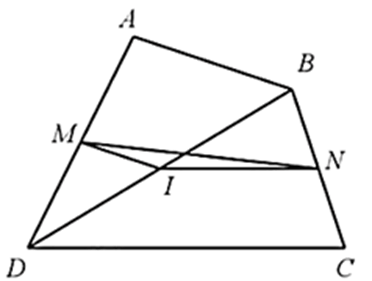
Lấy I là trung điểm của BD.
Xét ∆ABD có M, I lần lượt là trung điểm của AD, BD nên MI là đường trung bình của ∆ABD
Suy ra MI // AB và
Xét ∆BDC có N, I lần lượt là trung điểm của BC, BD nên NI là đường trung bình của ∆BDC
Suy ra NI // CD và
Do đó (1).
• Nếu I không thuộc MN thì MNI là tam giác nên ta có MN < MI + NI (bất đẳng thức tam giác).
• Nếu I thuộc MN ta có MN = MI + NI.
Tức là, ta luôn có MN ≤ MI + NI (2).
Từ (1), (2) suy ra
Dấu đẳng thức xảy ra khi I thuộc MN, khi đó AB // MI // CD.
Vậy dấu đẳng thức xảy ra khi AB // CD.
Lời giải SBT Toán 8 Bài 3: Đường trung bình của tam giác hay khác:
Bài 14 trang 65 SBT Toán 8 Tập 2: Chọn phát biểu đúng trong các phát biểu sau: a) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng một phần ba cạnh đó ....
Bài 15 trang 65 SBT Toán 8 Tập 2: Hình 21 cho biết cạnh của tam giác đều ABC bằng 6 cm; M, N lần lượt là trung điểm các cạnh AB, AC. Chỉ ra phát biểu sai trong các phát biểu sau: ....
Bài 16 trang 65 SBT Toán 8 Tập 2: Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tia Mx song song với AC cắt AB tại E và tia My song song với AB cắt AC tại F. Chứng minh: ....
Bài 17 trang 65 SBT Toán 8 Tập 2: Để làm cây thông noel, người ta hàn một khung sắt có dạng hình tam giác cân ABC (AB = AC = 2 m) cùng các thanh sắt nằm ngang GF, HE, ID, BC ....
Bài 18 trang 66 SBT Toán 8 Tập 2: Cho hình chữ nhật ABCD. Kẻ CH vuông góc với BD (H ∈ BD). Gọi I, K, M lần lượt là trung điềm của BH, CH, AD. Chứng minh: ....
Bài 19* trang 66 SBT Toán 8 Tập 2: Cho tứ giác ABCD có AD = BC. Đường thẳng đi qua trung điểm M và N lần lượt của các cạnh AB và CD cắt các đường thẳng AD và BC lần lượt tại E và F ....

