Cho hình chữ nhật ABCD. Kẻ CH vuông góc với BD (H ∈ BD). Gọi I, K, M lần lượt
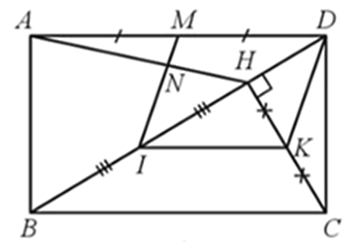
Cho hình chữ nhật ABCD. Kẻ CH vuông góc với BD (H ∈ BD). Gọi I, K, M lần lượt là trung điềm của BH, CH, AD. Chứng minh:
Giải SBT Toán 8 Bài 3: Đường trung bình của tam giác - Cánh diều
Bài 18 trang 66 SBT Toán 8 Tập 2: Cho hình chữ nhật ABCD. Kẻ CH vuông góc với BD (H ∈ BD). Gọi I, K, M lần lượt là trung điềm của BH, CH, AD. Chứng minh:
a) Tứ giác IKDM là hình bình hành;
b) Gọi N là giao điểm của IM và AH. Hỏi IN có thể là đường trung bình của tam giác HAB không? Vì sao?
Lời giải:
a) Xét ∆HBC có I, K lần lượt là trung điểm của BH, CH nên IK là đường trung bình của ∆HBC
Suy ra IK // BC và
Do ABCD là hình chữ nhật nên AD // BC, AD = BC, mà M ∈ AD nên MD // BC
Do đó, IK // MD (1)
Vì và (do M là trung điểm của AD, AD = BC) nên IK = MD (2)
Từ (1) và (2) suy ra tứ giác IKDM là hình bình hành.
b) Nếu IN là đường trung bình của tam giác HAB thì IN // AB. Suy ra IM // AB.
Xét ∆ABD có M là trung điểm của AD và IM // AB nên I là trung điểm của BD (3).
Mặt khác, theo giả thiết, I là trung điểm của HB (4).
Từ (3) và (4) suy ra vô lí.
Vậy IN không thể là đường trung bình của tam giác HAB.
Lời giải SBT Toán 8 Bài 3: Đường trung bình của tam giác hay khác: