Cho tam giác ABC vuông cân tại A Lấy điểm M thuộc cạnh huyền BC

---

Giải SBT Toán 8 Bài 5: Hình chữ nhật - Cánh diều

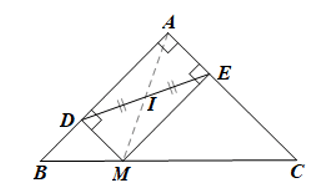
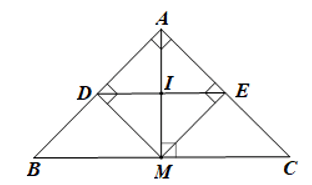
Bài 25 trang 97, 98 SBT Toán 8 Tập 1: Cho tam giác ABC vuông cân tại A. Lấy điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là hình chiếu của điểm M trên đường thẳng AB, AC.

a) Tứ giác ADME là hình gì? Vì sao?

b) Gọi I là trung điểm của DE. Chứng minh ba điểm A, I, M thẳng hàng.

c) Chứng minh khi điểm M thay đổi vị trí trên cạnh BC thì chu vi của tứ giác ADME không đổi.

d) Điểm M ở vị trí nào trên cạnh BC thì DE có độ dài nhỏ nhất? Tính độ dài nhỏ nhất đó, biết AB = 2 cm.

Lời giải:

a) Do D, E lần lượt là hình chiếu của điểm M trên đường thẳng AB, AC nên MD ⊥ AB, ME ⊥ AC.

Suy ra $\widehat{ADM}=\widehat{AEM}=90°$

Tam giác ABC vuông cân tại A nên $\widehat{BAC}=90°$

Tứ giác ADME có $\widehat{DAE}=\widehat{AEM}=\widehat{MDA}=90°$ nên ADME là hình chữ nhật.

b) Do ADME là hình chữ nhật nên hai đường chéo DE và AM cắt nhau tại trung điểm của mỗi đường.

Mà I là trung điểm của DE, suy ra I là trung điểm của AM.

Vậy ba điểm A, I, M thẳng hàng.

c) Do ADME là hình chữ nhật nên DM // AC.

Suy ra $\widehat{BMD}=\widehat{ACB}$ (hai góc so le trong).

Mà $\widehat{ABC}=\widehat{ACB}=45°$ (vì tam giác ABC vuông cân tại A), suy ra $\widehat{BMD}=\widehat{ABC}=45°$.

Do đó tam giác BDM cân tại D. Suy ra BD = DM.

Chu vi của hình chữ nhật ADME là:

2(AD + DM) = 2(AD + BD) = 2AB.

Mà AB không đổi nên chu vi của tứ giác ADME không đổi.

d) Do ADME là hình chữ nhật nên AM = DE.

Suy ra DE có độ dài nhỏ nhất khi AM có độ dài nhỏ nhất.

Vậy M là hình chiếu của A trên đường thẳng BC.

Trong tam giác ABC vuông cân tại A, ta có:

AC = AB = 2 cm và BC² = AB² + AC² = 2² + 2² = 8 (định lý Pythagore)

Suy ra $BC=\sqrt{8}\text{ cm}$.

Xét ∆ABM vuông tại M và ∆ACM vuông tại M có:

Cạnh AM chung, $\widehat{ABM}=\widehat{ACM}$ (do ∆ABC vuông cân tại A)

Do đó ∆ABM = ∆ACM (cạnh góc vuông – góc nhọn kề).

Suy ra $BM=CM=\frac{BC}{2}=\frac{\sqrt{8}}{2}=\sqrt{2}\text{ cm}$.

Tam giác ABM vuông tại M có $\widehat{ABM}=45°$ nên $\widehat{BAM}=\widehat{ABM}=45°$.

Suy ra tam giác ABM vuông cân tại M.

Do đó $DE=AM=BM=\sqrt{2}\left(\text{cm}\right)$.

Vậy $DE=\sqrt{2}\text{ cm}$.

Lời giải SBT Toán 8 Bài 5: Hình chữ nhật hay khác:

• Bài 21 trang 97 SBT Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? ....

• Bài 22 trang 97 SBT Toán 8 Tập 1: Hình 20 mô tả mặt cắt ngang tầng trệt của một ngôi nhà ....

• Bài 23 trang 97 SBT Toán 8 Tập 1: Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O ....

• Bài 24 trang 97 SBT Toán 8 Tập 1: Cho tam giác ABC cân tại A có các đường trung tuyến BM, CN cắt nhau tại G ....