Cho tam giác ABC có cạnh BC = 2x (dm), đường cao AH = x (dm) với x > 0

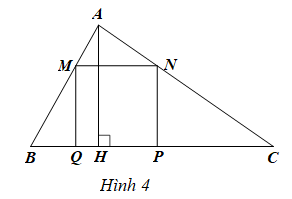
Cho tam giác ABC có cạnh BC = 2x (dm), đường cao AH = x (dm) với x > 0 và hình vuông MNPQ có cạnh MN = y (dm) với y > 0 (Hình 4).

Giải SBT Toán 8 Bài 4: Luyện tập hằng đẳng thức vào phân tích đa thức thành nhân tử - Cánh diều

Bài 26 trang 18 SBT Toán 8 Tập 1: Cho tam giác ABC có cạnh BC = 2x (dm), đường cao AH = x (dm) với x > 0 và hình vuông MNPQ có cạnh MN = y (dm) với y > 0 (Hình 4).

a) Viết công thức tính tổng diện tích của các tam giác AMN, BMQ, CNPdưới dạng tích.

b) Tính tổng diện tích của các tam giác AMN, BMQ, CNP, biết x ‒ y = 2và x + y = 10.

Lời giải:

a) Diện tích của tam giác ABC là:

$\frac{1}{2}.AH.BC=\frac{1}{2}.x.2x=x^2$ (dm²)

Diện tích hình vuông MNPQ là:

MN² = y² (dm²)

Vì vậy, tổng diện tích của các tam giác AMN, BMQ, CNP là:

S = x² ‒ y² (dm²)

b) Từ câu a, ta có

S = x² ‒ y² = (x ‒ y)(x + y)

Thay x – y = 2 và x + y = 10 vào S ta được:

S = 2.10 = 20 (dm²).

Vậy tổng diện tích của các tam giác AMN, BMQ, CNP là20 dm².

Lời giải SBT Toán 8 Bài 4: Luyện tập hằng đẳng thức vào phân tích đa thức thành nhân tử hay khác:

• Bài 22 trang 17 SBT Toán 8 Tập 1: Phân tích mỗi đa thức sau thành nhân tử: a) $25x^2-\frac{1}{4}$ ....

• Bài 23 trang 17 SBT Toán 8 Tập 1: Phân tích mỗi đa thức sau thành nhân tử: a) x³(13xy ‒ 5) ‒ y³(5 ‒ 13xy) ....

• Bài 24 trang 18 SBT Toán 8 Tập 1: Tính giá trị của mỗi biểu thức sau: a) $A=x^2+xy+\frac{y^2}{4}$ biết $x+\frac{y}{2}=100$ ....

• Bài 25* trang 18 SBT Toán 8 Tập 1: Chứng minh biểu thức B = x⁵ ‒ 15x² ‒ x + 5chia hết cho 5 với mọi số nguyên x ....