Cho góc xOy khác góc bẹt. Dùng thước hai lề (thước có hai cạnh song song)
Giải SBT Toán 8 Bài 6: Hình thoi - Cánh diều
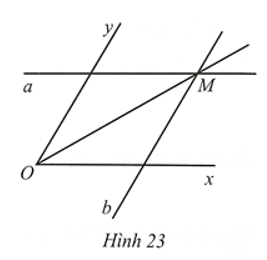
Bài 29 trang 100 SBT Toán 8 Tập 1: Cho góc xOy khác góc bẹt. Dùng thước hai lề (thước có hai cạnh song song). Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh Ox của góc xOy, vẽ đường thẳng a theo cạnh kia của thước. Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh Oy của góc xOy, vẽ đường thẳng b theo cạnh kia của thước. Hai đường thẳng a, b cắt nhau tại điểm M nằm trong góc xOy (Hình 23). Chứng minh tia OM là tia phân giác của góc xOy.
Lời giải:
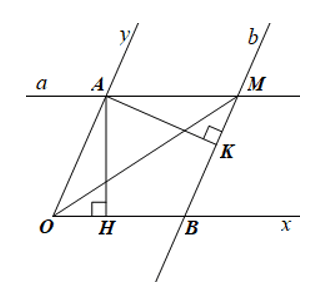
Gọi A là giao điểm của đường thẳng a với tia Oy, B là giao điểm của đường thẳng b với tia Ox.
Kẻ AH vuông góc với OB tại H, AK vuông góc với BM tại K.
Do khoảng cách giữa hai lề của thước là không đổi nên ta có AH = AK.
Do a // Ox nên AM // OB, b // Oy nên BM // OA
Tứ giác OAMB có AM // OB, BM // OA nên OAMB là hình bình hành.
Suy ra hay .
Trong ∆AOH vuông tại H có: ;
Trong ∆AMK vuông tại K có: .
Do đó .
Xét ∆AOH vuông tại H và ∆AMK vuông tại K có:
AH = AK,
Do đó ∆AOH = ∆AMK (cạnh góc vuông – góc nhọn kề).
Suy ra OA = MA (hai cạnh tương ứng)
Hình bình hành OAMB có OA = MA nên OAMB là hình thoi.
Từ đó suy ra OM là tia phân giác của góc xOy.
Lời giải SBT Toán 8 Bài 6: Hình thoi hay khác: