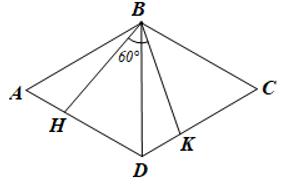
Cho hình thoi ABCD có AB = 2 cm, góc A = 1/2 góc B
Giải SBT Toán 8 Bài 6: Hình thoi - Cánh diều
Bài 30* trang 100 SBT Toán 8 Tập 1: Cho hình thoi ABCD có AB = 2 cm, . Các điểm H, K thay đổi lần lượt trên cạnh AD, CD sao cho .
a) Chứng minh DH + DK không đổi.
b) Xác định vị trí của các điểm H, K để độ dài HK ngắn nhất. Tính độ dài ngắn nhất đó.
Lời giải:
a) Do ABCD là hình thoi nên DA = AB = 2 cm, (BD là đường phân giác của góc ABC).
Mà , suy ra .
Do đó tam giác ABD cân tại D.
Suy ra DA = DB.
Mà AB = DA, suy ra AB = DA = DB.
Do đó tam giác ABD đều nên .
Suy ra (hai góc so le trong của AB // CD).
Ta có: ;
Suy ra .
Xét ∆ABH và ∆DBK có:
; AB = BD;
Do đó ∆ABH = ∆DBK (g.c.g).
Suy ra AH = DK (hai cạnh tương ứng).
Do đó DH + DK = DH + AH = AD (không đổi)
Vậy DH + DK không đổi.
b) Do ∆ABH = ∆DBK (câu a) nên BH = BK (hai cạnh tương ứng).
Tam giác BHK có BH = BK và nên tam giác BHK là tam giác đều.
Suy ra HK = BH = BK.
Do đó, độ dài HK ngắn nhất khi BH và BK ngắn nhất.
Khi đó H, K lần lượt là hình chiếu của B trên AD, CD.
Xét ∆ABH vuông tại H và ∆DBH vuông tại H có:
AB = BD, cạnh BH chung
Do đó ∆ABH = ∆DBH (cạnh huyền – cạnh góc vuông).
Suy ra .
Áp dụng định lý Pythagore cho tam giác ABH vuông tại H, ta có:
AB2 = AH2 + BH2
Suy ra BH2 = AB2 – AH2 = 22 – 12 = 4 – 1 = 3.
Do đó .
Vậy độ dài ngắn nhất của HK là .
Lời giải SBT Toán 8 Bài 6: Hình thoi hay khác: