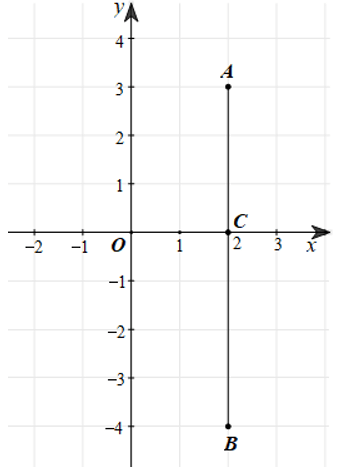Trong mặt phẳng toạ độ Oxy, cho các điểm A(2; 3), B(2 ; ‒4)
Giải SBT Toán 8 Bài tập cuối chương 3 - Cánh diều
Bài 31 trang 63 SBT Toán 8 Tập 1: Trong mặt phẳng toạ độ Oxy, cho các điểm A(2; 3), B(2 ; ‒4). Tìm toạ độ điểm C sao cho C nằm trên trục Ox và CA + CB đạt giá trị nhỏ nhất.
Lời giải:
Biểu diễn điểm A(2; 3), B(2 ; ‒4) trên mặt phẳng tọa độ Oxy như hình vẽ sau:
Khi C nằm trên trục Ox thì có 2 trường hợp xảy ra:
• Trường hợp 1: Ba điểm A, B, C không thẳng hàng, khi đó tạo thành tam giác ABC.
Theo bất đẳng thức tam giác ta có: CA + CB > AB.
• Trường hợp 2: Ba điểm A, B, C thẳng hàng, khi đó CA + CB = AB.
Từ 2 trường hợp trên ta được: CA + CB ≥ AB
Do đó CA + CB đạt giá trị nhỏ nhất bằng AB, khi ba điểm A, B, C thẳng hàng.
Khi đó, C là giao điểm của AB và trục Ox.
Vậy C(2; 0).
Lời giải SBT Toán 8 Bài tập cuối chương 3 hay khác:
Bài 28 trang 63 SBT Toán 8 Tập 1: Toạ độ giao điểm của hai đường thẳng ....
Bài 29 trang 63 SBT Toán 8 Tập 1: Cho đồ thị của hàm số y = ax + b đi qua điểm M(1; 4) ....