Cho tam giác ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm. Tia phân giác của góc BAC cắt BC

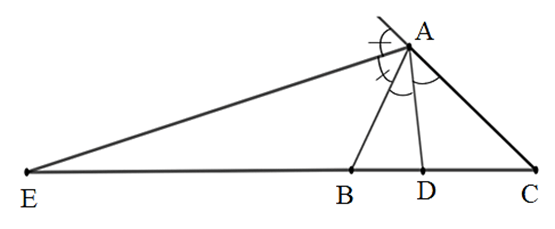
Cho ∆ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm. Tia phân giác của cắt BC tại D, tia phân giác của góc ngoài tại đỉnh A cắt BC tại E. Tính độ dài DB, DC, EB.

Giải sách bài tập Toán 8 Bài 3: Tính chất đường phân giác của tam giác - Chân trời sáng tạo

Bài 2 trang 48 sách bài tập Toán 8 Tập 2: Cho ∆ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm. Tia phân giác của $\widehat{BAC}$ cắt BC tại D, tia phân giác của góc ngoài tại đỉnh A cắt BC tại E. Tính độ dài DB, DC, EB.

Lời giải:

• Vì AD là phân giác của $\widehat{BAC}$ trong ∆ABC nên ta có

$\frac{DB}{DC}=\frac{AB}{AC}=\frac{6}{9}=\frac{2}{3}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{DB}{2}=\frac{DC}{3}=\frac{DB+DC}{2+3}=\frac{BC}{5}=\frac{10}{5}$ = 2.

Suy ra $\frac{DB}{2}$ = 2 và $\frac{DC}{3}$ = 2.

Do đó DB = 4 cm; DC = 6 cm.

• Vì AE là phân giác ngoài tại đỉnh A của ∆ABC nên ta có

$\frac{EB}{EC}=\frac{AB}{AC}=\frac{6}{9}=\frac{2}{3}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{EC}{3}=\frac{EB}{2}=\frac{EC-EB}{3-2}=\frac{BC}{1}$ = 10.

Do đó $\frac{EB}{2}$ = 10 suy ra EB = 20 cm.

Vậy DB = 4 cm, DC = 6 cm, EB = 20 cm.

Lời giải SBT Toán 8 Bài 3: Tính chất đường phân giác của tam giác hay khác:

• Bài 1 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC vuông tại A. Tia phân giác của $\widehat{BAC}$ cắt BC tại D. Cho biết DB = 15cm, DC = 20 cm Tính độ dài AB, AC ...

• Bài 3 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC có các đường phân giác AD, BE, CF (D ∈ BC, E ∈ AC, F ∈ AB) cắt nhau tại I. Chứng minh: ...

• Bài 4 trang 48 sách bài tập Toán 8 Tập 2: Cho hình bình hành ABCD có tia phân giác của góc A cắt đường chéo BD tại M và phân giác của góc D cắt đường chéo AC tại N ...

• Bài 5 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC cân ở A. Tia phân giác của $\widehat{ABC}$ cắt AC tại D. Cho biết BC= 10 cm, AB = 15 cm. Tính DA, DC ...

• Bài 6 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC có đường trung tuyến AM (M ∈ BC). Tia phân giác của $\widehat{AMB}$ cắt AB tại D, tia phân giác của $\widehat{AMC}$ cắt AC tại E ...