Cho hình bình hành ABCD có tia phân giác của góc A cắt đường chéo BD tại M

Cho hình bình hành ABCD có tia phân giác của góc A cắt đường chéo BD tại M và phân giác của góc D cắt đường chéo AC tại N. Chứng minh MN // AD.

Giải sách bài tập Toán 8 Bài 3: Tính chất đường phân giác của tam giác - Chân trời sáng tạo

Bài 4 trang 48 sách bài tập Toán 8 Tập 2: Cho hình bình hành ABCD có tia phân giác của góc A cắt đường chéo BD tại M và phân giác của góc D cắt đường chéo AC tại N. Chứng minh MN // AD.

Lời giải:

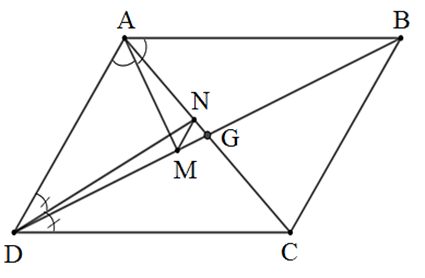
Gọi G là giao điểm của AC và BD.

• Vì DN là phân giác của $\widehat{ADC}$ trong ∆ADC nên $\frac{NA}{NC}=\frac{AD}{DC}$.

• Vì AM là phân giác của $\widehat{BAD}$ trong ∆ABD nên $\frac{MD}{MB}=\frac{AD}{AB}$ = $\frac{AD}{DC}$ (vì AB = DC).

Suy ra $\frac{MD}{MB}=\frac{NA}{NC}$.

Do đó $\frac{NA}{MD}=\frac{NC}{MB}=\frac{NA+NC}{MD+MB}=\frac{AC}{BD}=\frac{AG}{DG}$ (AC = 2AG; BD = 2BG)

Khi đó $\frac{NA}{AG}=\frac{MD}{DG}$.

Xét ∆AGD có $\frac{NA}{AG}=\frac{MD}{DG}$ nên theo định lí Thalès đảo, ta có MN // AD.

Lời giải SBT Toán 8 Bài 3: Tính chất đường phân giác của tam giác hay khác:

• Bài 1 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC vuông tại A. Tia phân giác của $\widehat{BAC}$ cắt BC tại D. Cho biết DB = 15cm, DC = 20 cm Tính độ dài AB, AC ...

• Bài 2 trang 48 sách bài tập Toán 8 Tập 2: Cho ∆ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm. Tia phân giác của $\widehat{BAC}$ cắt BC tại D, tia phân giác của góc ngoài tại đỉnh A ...

• Bài 3 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC có các đường phân giác AD, BE, CF (D ∈ BC, E ∈ AC, F ∈ AB) cắt nhau tại I. Chứng minh: ...

• Bài 5 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC cân ở A. Tia phân giác của $\widehat{ABC}$ cắt AC tại D. Cho biết BC= 10 cm, AB = 15 cm. Tính DA, DC ...

• Bài 6 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC có đường trung tuyến AM (M ∈ BC). Tia phân giác của $\widehat{AMB}$ cắt AB tại D, tia phân giác của $\widehat{AMC}$ cắt AC tại E ...