Chứng minh rằng trong một tứ giác độ dài mỗi cạnh bé hơn tổng độ dài ba cạnh còn lại
Chứng minh rằng trong một tứ giác, độ dài mỗi cạnh bé hơn tổng độ dài ba cạnh còn lại.
Giải sách bài tập Toán 8 Bài 10: Tứ giác - Kết nối tri thức
Bài 3.2 trang 32 sách bài tập Toán 8 Tập 1: Chứng minh rằng trong một tứ giác, độ dài mỗi cạnh bé hơn tổng độ dài ba cạnh còn lại.
Lời giải:
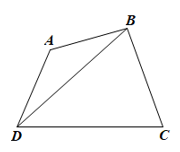
Xét tứ giác ABCD như hình vẽ. Ta cần chứng minh AB < AD + BC + CD và các trường hợp còn lại tương tự.
Xét tam giác ABD, ta có: AB < AD + DB (bất đẳng thức trong tam giác).
Xét tam giác BCD, ta có: DB < BC + CD (bất đẳng thức trong tam giác).
Do đó AB < AD + DB < AD + BC + CD.
Vậy AB < AD + BC + CD.
Tương tự ta cũng có:
BC < AB + CD + DA; CD < AD + AB + BC; DA < AB + BC + CD.
Lời giải SBT Toán 8 Bài 10: Tứ giác hay khác: