Chứng minh tổng độ dài hai đường chéo của tứ giác
Chứng minh tổng độ dài hai đường chéo của tứ giác:
Giải sách bài tập Toán 8 Bài 10: Tứ giác - Kết nối tri thức
Bài 3.3 trang 32 sách bài tập Toán 8 Tập 1: Chứng minh tổng độ dài hai đường chéo của tứ giác:
a) Bé hơn chu vi của tứ giác;
b) Lớn hơn tổng hai cạnh đối tuỳ ý của tứ giác, từ đó lớn hơn nửa chu vi của tứ giác.
Lời giải:
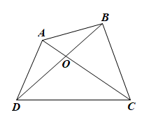
Xét tứ giác ABCD. Chu vi tứ giác ABCD là PABCD = AB + BC + CD + DA.
a) Trong ∆ABC có AC < AB + BC (bất đẳng thức trong tam giác)
Trong ∆ACD có AC < CD + DA (bất đẳng thức trong tam giác)
Do đó AC + AC < AB + BC + CD + DA hay 2AC < PABCD (1)
Tương tự, trong ∆ABD có BD < AD + AB
Trong ∆BCD có: BD < CD + BC
Do đó BD + BD < AD + AB + CD + BC hay 2BD < PABCD. (2)
Từ (1) và (2) suy ra 2(AC + BD) < 2PABCD, do đó AC + BD < PABCD.
b) Gọi O là giao điểm của AC và BD.
Trong ∆OAB có OA + OB > AB (bất đẳng thức trong tam giác)
Trong ∆OCD có OC + OD > CD (bất đẳng thức trong tam giác)
Nên AC + BD = OA + OC + OB + OD > AB + CD.
Trong ∆OAD có OA + OD > AD (bất đẳng thức trong tam giác)
Trong ∆OBC có OB + OC > BC (bất đẳng thức trong tam giác)
Nên AC + BD = OA + OC + OB + OD > AD + BC.
Vậy 2(AC + BD) > AB + BC + CD + DA = PABCD
Tức là
Lời giải SBT Toán 8 Bài 10: Tứ giác hay khác: