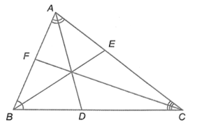
Cho ∆ABC có AD, BE, CF lần lượt là đường phân giác của góc A, góc B, góc C

Cho ∆ABC có AD, BE, CF lần lượt là đường phân giác của góc A, góc B, góc C (D ∈ BC, E ∈ AC, F ∈ AB). Chứng minh rằng:

Giải sách bài tập Toán 8 Bài 17: Tính chất đường phân giác của tam giác - Kết nối tri thức

Bài 4.13 trang 52 sách bài tập Toán 8 Tập 1: Cho ∆ABC có AD, BE, CF lần lượt là đường phân giác của góc A, góc B, góc C (D ∈ BC, E ∈ AC, F ∈ AB). Chứng minh rằng: $\frac{AE}{EC}\cdot \frac{CD}{DB}\cdot \frac{BF}{FA}=1.$

Lời giải:

Trong ∆ABC có AD là phân giác của $\widehat{BAC}$ nên $\frac{DC}{DB}=\frac{AC}{AB}$ (tính chất đường phân giác của tam giác).

Tương tự, ta có BE, CF lần lượt là tia phân giác của $\widehat{B},\widehat{C}$.

Suy ra $\frac{EA}{EC}=\frac{BA}{BC};\frac{FB}{FA}=\frac{CB}{CA}$.

Do đó: $\frac{AE}{EC}\cdot \frac{CD}{DB}\cdot \frac{BF}{FA}=\frac{BA}{BC}\cdot \frac{AC}{AB}\cdot \frac{CB}{CA}=1$

Lời giải SBT Toán 8 Bài 17: Tính chất đường phân giác của tam giác hay khác:

• Bài 4.11 trang 52 sách bài tập Toán 8 Tập 1: Tìm độ dài x trong Hình 5.12 ...

• Bài 4.12 trang 52 sách bài tập Toán 8 Tập 1: Cho tam giác ABC, trung tuyến AI. Tia phân giác góc AIB và tia phân giác góc AIC cắt AB, AC lần lượt tại M và N ...

• Bài 4.14 trang 52 sách bài tập Toán 8 Tập 1: Cho tam giác ABC, phân giác AD (D ∈ BC). Kẻ DE // AB (E ∈ AC) ...