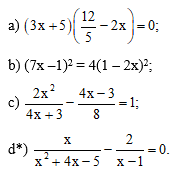Bài 2 trang 9 SBT Toán 9 Tập 1

---

Giải các phương trình:

Giải SBT Toán 9 Bài 1: Phương trình quy về phương trình bậc nhất một ẩn - Cánh diều

Bài 2 trang 9 SBT Toán 9 Tập 1: Giải các phương trình:

Lời giải:

a) $\left(3x+5\right)\left(\frac{12}{5}-2x\right)=0$

3x + 5 = 0 hoặc $\frac{12}{5}-2x=0$

3x = –5 hoặc $-2x=-\frac{12}{5}$

$x=-\frac{5}{3}$ hoặc $x=\frac{6}{5}.$

Vậy phương trình đã cho có 2 nghiệm là $x=-\frac{5}{3}$ và $x=\frac{6}{5}.$

b) (7x ‒1)² = 4(1 ‒ 2x)²

(7x ‒ 1)² ‒ 4(1 ‒ 2x)² = 0

(7x ‒ 1)² ‒ [2.(1 ‒ 2x)]² = 0

(7x ‒ 1)² ‒ (2 ‒ 4x)² = 0

[(7x ‒ 1) ‒ (2 ‒ 4x)].[(7x ‒1) + (2 ‒ 4x)] = 0

[7x – 1 – 2 + 4x].[7x – 1 + 2 – 4x] = 0

(11x ‒ 3)(3x + 1) = 0

11x ‒ 3 = 0 hoặc 3x + 1 = 0

11x = 3 hoặc 3x = –1

$x=\frac{3}{11}$ hoặc $x=-\frac{1}{3}$

Vậy phương trình đã cho có hai nghiệm $x=\frac{3}{11}$ và $x=-\frac{1}{3}$

c) Điều kiện xác định của phương trình: $x\ne -\frac{3}{4}.$

$\frac{2x^2}{4x+3}-\frac{4x-3}{8}=1$

$\frac{8\cdot 2x^2}{8\left(4x+3\right)}-\frac{\left(4x+3\right)\left(4x-3\right)}{8\left(4x+3\right)}=\frac{8\left(4x+3\right)}{8\left(4x+3\right)}$

8.2x² – (4x + 3)(4x – 3) = 8(4x + 3)

16x² ‒ (16x² ‒ 9) = 32x + 24

16x² ‒ 16x² + 9 = 32x + 24

‒32x = 24 – 9

‒32x = 15

$x=-\frac{15}{32}$

Ta thấy $x=-\frac{15}{32}$ thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm $x=-\frac{15}{32}$.

d*) Ta có:

x² + 4x ‒ 5 = (x² + 4x + 4) ‒ 9

= (x + 2)² ‒ 3² = (x + 2 – 3)(x + 2 + 3)

= (x ‒ 1)(x + 5).

Điều kiện xác định: x ≠ 1 và x ≠ ‒5.

$\frac{x}{x^2+4x-5}-\frac{2}{x-1}=0$

$\frac{x}{\left(x-1\right)\left(x+5\right)}-\frac{2\left(x+5\right)}{\left(x-1\right)\left(x+5\right)}=0$

x ‒ 2(x + 5) = 0

x ‒ 2x ‒ 10 = 0

‒x = 10

x = ‒10.

Ta thấy x = ‒10 thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm x = ‒10.

Lời giải SBT Toán 9 Bài 1: Phương trình quy về phương trình bậc nhất một ẩn hay khác:

• Bài 1 trang 9 SBT Toán 9 Tập 1: Tìm điều kiện xác định của mỗi phương trình sau: a) $\frac{13}{4-x^2}=1;$....

• Bài 3 trang 9 SBT Toán 9 Tập 1: Một ô tô đi quãng đường AB dài 61,5 km. Sau khi đi được 30 km với tốc độ không đổi, ô tô đi tiếp quãng đường còn lại với tốc độ tăng thêm 2 km/h...

• Bài 4 trang 9 SBT Toán 9 Tập 1: Một ca nô đi xuôi dòng từ địa điểm A đến địa điểm B, rồi lại đi ngược dòng từ địa điểm B trở về địa điểm A....

• Bài 5 trang 10 SBT Toán 9 Tập 1: Cho một phân số có mẫu số lớn hơn tử số là 2. Nếu bớt tử số đi 3 đơn vị và bớt mẫu số đi 6 đơn vị thì ta được một phân số mới bằng phân số nghịch đảo của phân số đã cho....

• Bài 6 trang 10 SBT Toán 9 Tập 1: Biết khối lượng riêng của kim loại A lớn hơn khối lượng riêng của kim loại B là 6,24 kg/m³....

• Bài 7 trang 10 SBT Toán 9 Tập 1: Bác Lan dự định dùng hết số tiền 480 nghìn đồng để mua gạo nếp gói bánh chưng nhân dịp tết Nguyên đán. ...

• Bài 8 trang 10 SBT Toán 9 Tập 1: Một mảnh vườn có dạng hình chữ nhật với chiều rộng là 10 m. Chủ vườn đã làm con đường thảm cỏ (phần tô màu xám) với các kích thước như Hình 2.....