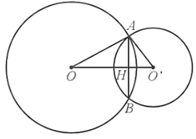
Cho hai đường tròn (O; 17 cm) và (O’; 10 cm) cắt nhau tại A và B, Biết rằng OO’ = 21 cm
Cho hai đường tròn (O; 17 cm) và (O’; 10 cm) cắt nhau tại A và B. Biết rằng OO’ = 21 cm. Tính độ dài đoạn thẳng AB.
Giải SBT Toán 9 Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn - Cánh diều
Bài 4 trang 102 SBT Toán 9 Tập 1: Cho hai đường tròn (O; 17 cm) và (O’; 10 cm) cắt nhau tại A và B. Biết rằng OO’ = 21 cm. Tính độ dài đoạn thẳng AB.
Lời giải:
Gọi H là giao điểm của OO’ với AB (hình vẽ).
Ta có OA = OB (bán kính đường tròn tâm O) và O’A = O’B (bán kính đường tròn tâm O’)
Suy ra OO’là đường trung trực của đoạn thẳng AB.
Do đó OO’ ⊥ AB tại trung điểm H của AB.
Đặt OH = x(cm) thì O’H = OO’ – OH = 21 ‒ x(cm).
Xét ∆OAH vuông tại H, theo định lí Pythagore, ta có:
OA2 = AH2 + OH2, suy ra AH2 = OA2 ‒ OH2.
Xét ∆O’AH vuông tại H, theo định lí Pythagore, ta có:
O’A2 = AH2 + O’H2, suy ra AH2 = O’A2 ‒ O’H2.
Do đó OA2 ‒ OH2 = O’A2 ‒ O’H2
Suy ra: 172 ‒ x2 = 102 ‒ (21 ‒ x)2
289 – x2 = 100 – 441 + 42x – x2
42x = 630
x = 15 (cm).
Do đó AH2 = OA2 ‒ OH2 = 172 – x2 = 172 – 152 = 64.
Suy ra
Mà H là trung điểm của AB nên AB = 2AH = 2.8 = 16 cm.
Vậy AB = 16 cm.
Lời giải SBT Toán 9 Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn hay khác: