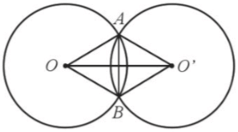
Cho hai đường tròn (O) và (O’) có bán kính bằng nhau, cắt nhau tại A và B
Cho hai đường tròn (O) và (O’) có bán kính bằng nhau, cắt nhau tại A và B. Chứng minh tứ giác OAO’B là hình thoi; từ đó, suy ra AB cắt OO’ tại trung điểm của mỗi đường.
Giải SBT Toán 9 Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn - Cánh diều
Bài 5 trang 102 SBT Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) có bán kính bằng nhau, cắt nhau tại A và B. Chứng minh tứ giác OAO’B là hình thoi; từ đó, suy ra AB cắt OO’ tại trung điểm của mỗi đường.
Lời giải:
Tứ giác OAO’B có OA = OB = O’A = O’B (cùng bằng bán kính của (O) và (O’))
Suy ra tứ giác OAO’B là hình thoi.
Do đó hai đường chéo AB và OO’ cắt nhau tại trung điểm của mỗi đường.
Lời giải SBT Toán 9 Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn hay khác: