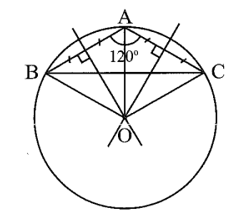
Cho tam giác ABC có AB = AC = 12 cm và góc BAC = 120 độ

Cho tam giác ABC có AB = AC = 12 cm và Xác định tâm và tính bán kính của đường tròn (O; R) ngoại tiếp tam giác ABC.

Giải sách bài tập Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Chân trời sáng tạo

Bài 1 trang 79 sách bài tập Toán 9 Tập 2: Cho tam giác ABC có AB = AC = 12 cm và $\widehat{BAC}=120°.$ Xác định tâm và tính bán kính của đường tròn (O; R) ngoại tiếp tam giác ABC.

Lời giải:

Vẽ đường trung trực của đoạn thẳng AB và AC cắt nhau tại điểm O.

Khi đó OA = OB và OA = OC.

Do đó R = OA = OB = OC, suy ra đường tròn (O; R) ngoại tiếp tam giác ABC.

Ta có AB = AC và OB = OC nên OA là đường trung trực của đoạn thẳng BC.

Vì tam giác ABC cân tại A nên đường trung trực OA của tam giác cũng là tia phân giác của góc BAC, suy ra $\widehat{OAB}=\frac{1}{2}\widehat{BAC}=\frac{1}{2}\cdot 120°=60°.$

Xét ∆OAB cân tại O (OA = OB) có $\widehat{OAB}=60°$ nên tam giác OAB là tam giác đều.

Vậy R = OA = AB = 12 (cm).

Lời giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay khác:

• Bài 2 trang 79 sách bài tập Toán 9 Tập 2: Cho tam giác ABC có đường cao AH (H ∈ BC) và nội tiếp đường tròn (O). ...

• Bài 3 trang 79 sách bài tập Toán 9 Tập 2: Cho hình chữ nhật ABCD có AB = 5 cm, AD = 12 cm. Tìm tâm và bán kính của đường tròn ngoại tiếp các tam giác ABC và ADC. ..

• Bài 4 trang 79 sách bài tập Toán 9 Tập 2: Cho tam giác đều MNP có cạnh bằng $2a\sqrt{3}.$ Tính theo a bán kính các đường tròn ngoại tiếp và nội tiếp tam giác MNP...

• Bài 5 trang 79 sách bài tập Toán 9 Tập 2: Để giữ vệ sinh trong một khu hội chợ, cứ mỗi cụm 3 quầy hàng A, B, C người ta lại đặt một thùng rác tại điểm O cách đều A, B, C. ...