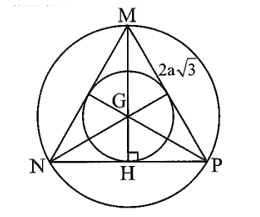
Cho tam giác đều MNP có cạnh bằng 2a căn bậc hai 3 Tính theo a bán kính các đường tròn ngoại tiếp

Cho tam giác đều MNP có cạnh bằng Tính theo a bán kính các đường tròn ngoại tiếp và nội tiếp tam giác MNP

Giải sách bài tập Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Chân trời sáng tạo

Bài 4 trang 79 sách bài tập Toán 9 Tập 2: Cho tam giác đều MNP có cạnh bằng $2a\sqrt{3}.$ Tính theo a bán kính các đường tròn ngoại tiếp và nội tiếp tam giác MNP

Lời giải:

Gọi G là trọng tâm, MH là đường cao của tam giác đều MNP.

Khi đó, đường tròn (G; GM) là đường tròn ngoại tiếp tam giác đều MNP; đường tròn (G; GH) là đường tròn nội tiếp tam giác đều MNP.

Xét ∆MNP đều có MH là đường cao nên đồng thời là đường trung tuyến, hay H là trung điểm của NP, do đó $NH=PH=\frac{1}{2}NP=\frac{1}{2}\cdot 2a\sqrt{3}=a\sqrt{3}.$

Xét ∆MNH vuông tại H, theo định lí Pythagore, ta có:

MN² = MH² + NH²

Suy ra $M{H}^2=M{N}^2-N{H}^2={\left(2a\sqrt{3}\right)}^2-{\left(a\sqrt{3}\right)}^2=3a.$

Do đó $MG=\frac{2}{3}MH=\frac{2}{3}\cdot 3a=2a;GH=\frac{1}{3}MH=\frac{1}{3}\cdot 3a=a.$

Vậy bán kính các đường tròn ngoại tiếp và nội tiếp tam giác MNP lần lượt là 2a và a.

Lời giải SBT Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay khác:

• Bài 1 trang 79 sách bài tập Toán 9 Tập 2: Cho tam giác ABC có AB = AC = 12 cm và $\widehat{BAC}=120°.$ Xác định tâm và tính bán kính của đường tròn (O; R) ngoại tiếp tam giác ABC...

• Bài 2 trang 79 sách bài tập Toán 9 Tập 2: Cho tam giác ABC có đường cao AH (H ∈ BC) và nội tiếp đường tròn (O). ...

• Bài 3 trang 79 sách bài tập Toán 9 Tập 2: Cho hình chữ nhật ABCD có AB = 5 cm, AD = 12 cm. Tìm tâm và bán kính của đường tròn ngoại tiếp các tam giác ABC và ADC. ..

• Bài 5 trang 79 sách bài tập Toán 9 Tập 2: Để giữ vệ sinh trong một khu hội chợ, cứ mỗi cụm 3 quầy hàng A, B, C người ta lại đặt một thùng rác tại điểm O cách đều A, B, C. ...