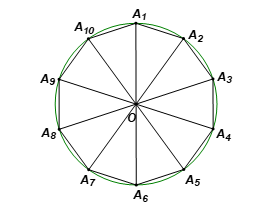
Cho đường tròn (O; R). Lấy các điểm A1, A2, A2, …, A10 trên đường tròn (O; R)

Cho đường tròn (O; R). Lấy các điểm A là một đa giác đều.

Giải sách bài tập Toán 9 Bài 3: Đa giác đều và phép quay - Chân trời sáng tạo

Bài 1 trang 86 sách bài tập Toán 9 Tập 2: Cho đường tròn (O; R). Lấy các điểm A₁, A₂, A₂, …, A₁₀ trên đường tròn (O; R) sao cho các điểm này chia đường tròn thành 10 cung có số đo bằng nhau. Chứng minh đa giác A₁A₂ A₃…A₁₀ là một đa giác đều.

Lời giải:

⦁ Các điểm A₁, A₂, A₃, …, A₁₀ chia đường tròn thành 10 cung bằng nhau, mỗi cung có số đo bằng $\frac{360°}{10}=36°,$ do dó $\widehat{A_{1}O{A}_2}=\widehat{A_{2}O{A}_3}=\mathrm{...}=\widehat{A_{10}O{A}_1}=36°.$

Xét ∆OA₁A₂ và ∆OA₂A₃ có:

OA₁ = OA₂; $\widehat{A_{1}O{A}_2}=\widehat{A_{2}O{A}_3};$ OA₂ = OA₃

Do đó ∆OA₁A₂ = ∆OA₂A₃ (c.g.c).

Suy ra A₁A₂ = A₂A₃ (hai cạnh tương ứng).

Chứng minh tương tự, ta có 10 tam giác cân OA₁A₂, OA₂A₃,…, OA₁₀A₁ bằng nhau vì cùng có hai cạnh bằng R và góc ở đỉnh bằng 36°, suy ra A₁A₂ = A₂A₃ = … = A₁₀A₁ nên đa giác có các cạnh bằng nhau.

⦁ Xét ∆OA₁A₂ cân tại O (do OA₁ = OA₂) nên

$\widehat{O{A}_1{A}_2}=\widehat{O{A}_2{A}_1}=\frac{180°-\widehat{A_{1}O{A}_2}}{2}=\frac{180°-36°}{2}=72°.$

Tương tự, ta cũng có ∆OA₂A₃ cân tại O (do OA₂ = OA₃) nên

$\widehat{O{A}_2{A}_3}=\widehat{O{A}_3{A}_2}=\frac{180°-\widehat{A_{2}O{A}_3}}{2}=\frac{180°-36°}{2}=72°.$

Suy ra $\widehat{A_1{A}_2{A}_3}=\widehat{O{A}_2{A}_1}+\widehat{O{A}_2{A}_3}=72°+72°=144°.$

Do đó ta tính được mỗi góc của đa giác A₁A₂A₃…A₁₀ bằng 144°.

Vậy đa giác A₁A₂A₃... A₁₀ có các cạnh bằng nhau và các góc bằng nhau nên là một đa giác đều.

Lời giải SBT Toán 9 Bài 3: Đa giác đều và phép quay hay khác:

• Bài 2 trang 86 sách bài tập Toán 9 Tập 2: Các hình phẳng đều có trong Hình 10 cho ta hình ảnh của đa giác đều nào? Tính số đo góc của đa giác đều đó. ...

• Bài 3 trang 86 sách bài tập Toán 9 Tập 2: Dựa trên gợi ý của hình ngũ giác đều (Hình 11a), tìm phép quay biến hình con sao biển thành chính nó (Hình 11b). ...

• Bài 4 trang 86 sách bài tập Toán 9 Tập 2: Ngũ giác đài hay Lầu năm góc là trụ sở Bộ Quốc phòng Hoa Kỳ có dạng hình ngũ giác đều với độ dài cạnh khoảng 280 m như Hình 12...

• Bài 5 trang 87 sách bài tập Toán 9 Tập 2: Cho hình vuông ABCD cạnh a có O là giao điểm của hai đường chéo. Chứng minh có đường tròn (O; R) đi qua các đỉnh của hình vuông và có đường tròn (O; r) ...

• Bài 6 trang 87 sách bài tập Toán 9 Tập 2: Hình ảnh những bông hoa dưới đây là hình phẳng đều tương tự các đa giác đều nào?...