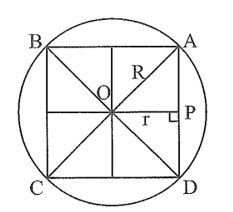
Cho hình vuông ABCD cạnh a có O là giao điểm của hai đường chéo. Chứng minh có đường tròn (O; R)

Cho hình vuông ABCD cạnh a có O là giao điểm của hai đường chéo. Chứng minh có đường tròn (O; R) đi qua các đỉnh của hình vuông và có đường tròn (O; r) tiếp xúc với các cạnh của hình vuông. Tính theo a bán kính R và r.

Giải sách bài tập Toán 9 Bài 3: Đa giác đều và phép quay - Chân trời sáng tạo

Bài 5 trang 87 sách bài tập Toán 9 Tập 2: Cho hình vuông ABCD cạnh a có O là giao điểm của hai đường chéo. Chứng minh có đường tròn (O; R) đi qua các đỉnh của hình vuông và có đường tròn (O; r) tiếp xúc với các cạnh của hình vuông. Tính theo a bán kính R và r.

Lời giải:

⦁ Vì ABCD là hình vuông nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường. Do đó OA = OB = OC = OD và AC ⊥ BD.

Vì ABCD là hình vuông ABCD nên nó nội tiếp đường tròn (O; R) với bán kính là $R=OA=OB=OC=OD=\frac{a\sqrt{2}}{2}.$

⦁ Trong tam giác AOD vuông cân tại O (do OA = OD và $\widehat{AOD}=90°$), vẽ đường cao OP, khi đó OP cũng đồng thời là đường trung tuyến của tam giác AOD.

Do đó $OP=\frac{AD}{2}=\frac{a}{2}$ (tính chất đường trung tuyến ứng với cạnh huyền).

Tương tự, ta có điểm O cách đều các cạnh của hình vuông một khoảng $\frac{a}{2}.$

Do đó, đường tròn (O; r) với $r=\frac{a}{2}$ tiếp xúc với các cạnh của hình vuông ABCD.

Lời giải SBT Toán 9 Bài 3: Đa giác đều và phép quay hay khác:

• Bài 1 trang 86 sách bài tập Toán 9 Tập 2: Cho đường tròn (O; R). Lấy các điểm A₁, A₂, A₂, …, A₁₀ trên đường tròn (O; R) sao cho các điểm này chia đường tròn thành 10 cung có số đo bằng nhau...

• Bài 2 trang 86 sách bài tập Toán 9 Tập 2: Các hình phẳng đều có trong Hình 10 cho ta hình ảnh của đa giác đều nào? Tính số đo góc của đa giác đều đó. ...

• Bài 3 trang 86 sách bài tập Toán 9 Tập 2: Dựa trên gợi ý của hình ngũ giác đều (Hình 11a), tìm phép quay biến hình con sao biển thành chính nó (Hình 11b). ...

• Bài 4 trang 86 sách bài tập Toán 9 Tập 2: Ngũ giác đài hay Lầu năm góc là trụ sở Bộ Quốc phòng Hoa Kỳ có dạng hình ngũ giác đều với độ dài cạnh khoảng 280 m như Hình 12...

• Bài 6 trang 87 sách bài tập Toán 9 Tập 2: Hình ảnh những bông hoa dưới đây là hình phẳng đều tương tự các đa giác đều nào?...