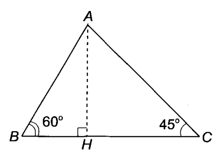
Cho tam giác ABC có đường cao AH, góc B = 60 độ và góc C bằng 45 độ cạnh BC = 6 cm

Cho tam giác ABC có đường cao AH, và cạnh BC = 6 cm. Chứng minh rằng AH = cm.

Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài tập cuối chương 4 - Kết nối tri thức

Bài 4.32 trang 52 sách bài tập Toán 9 Tập 1: Cho tam giác ABC có đường cao AH, $\widehat{B}=60°, \widehat{C} =45°$ và cạnh BC = 6 cm. Chứng minh rằng AH = $3\left(3-\sqrt{3}\right)$ cm.

Lời giải:

Xét tam giác ABH vuông tại H ta có:

$AH=BH.\tan B=BH.\tan 60°=BH\sqrt{3}$ hay $BH=\frac{AH}{\sqrt{3}}$

Xét tam giác ACH vuông cân tại H nên AH = CH.

Ta có BC = BH + CH hay 6 = $\frac{AH}{\sqrt{3}}+AH$$=AH.\left(\frac{1}{\sqrt{3}}+1\right)$

Do đó $AH=\frac{6}{\frac{1}{\sqrt{3}}+1}=3\left(3-\sqrt{3}\right)$ (cm) (đpcm).

Lời giải SBT Toán 9 Bài tập cuối chương 4 hay khác:

• Bài 1 trang 50 sách bài tập Toán 9 Tập 1: Tam giác ABC vuông tại A thì: sin B + cos C = 0. ...

• Bài 2 trang 50 sách bài tập Toán 9 Tập 1: Tam giác ABC vuông tại A thì: tan B + tan C = 0. ...

• Bài 3 trang 51 sách bài tập Toán 9 Tập 1: Chọn câu sai: Góc nhọn α có sin α = $\frac{1}{2}$ thì ...

• Bài 4.28 trang 51 sách bài tập Toán 9 Tập 1: Chứng minh nếu một góc nhọn của một tam giác vuông có số đo gấp đôi số đo góc nhọn kia thì tam giác đó có một cạnh dài gấp đôi một trong hai cạnh còn lại ...

• Bài 4.29 trang 51 sách bài tập Toán 9 Tập 1: Xét điểm B nằm giữa hai điểm A và H. Giả sử có điểm D sao cho DH vuông góc với AB và $\widehat{DAH}$ = 15°, $\widehat{DBH}$ = 30° ...

• Bài 4.30 trang 51 sách bài tập Toán 9 Tập 1: Cho hai toà nhà cách nhau 32 m. Tại điểm A trên nóc toà nhà cao nhìn xuống nóc D và chân C của toà nhà thấp lần lượt ...

• Bài 4.31 trang 51 sách bài tập Toán 9 Tập 1: Chiều cao từ mặt đất đến đỉnh tháp Pisa ở Italia là 58 mét, tháp nghiêng góc 5°30' đối với phương thẳng đứng (H.4.17) ...

• Bài 4.33 trang 52 sách bài tập Toán 9 Tập 1: Tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước (không đo trực tiếp được), biết khoảng cách từ một địa điểm C đến A và đến B là CA = 90 m ...

• Bài 4.34 trang 52 sách bài tập Toán 9 Tập 1: Một cầu thủ đứng cách khung thành 18 m, đá quả bóng sát mặt đất, nghiêng một góc 20° so với phương vuông góc với khung thành ...

• Bài 4.35 trang 52 sách bài tập Toán 9 Tập 1: Hai chiếc thuyền A và B ở vị trí được minh hoạ như trong Hình 4.20. Tính khoảng cách giữa chúng (làm tròn đến m), biết IK = 380 m ...

• Bài 4.36 trang 52 sách bài tập Toán 9 Tập 1: Tìm độ dài dây cáp mắc giữa hai cọc ở vị trí C, D trên hai bên bờ vực như trong Hình 4.21 (làm tròn đến mét) ...

• Bài 4.37 trang 52 sách bài tập Toán 9 Tập 1: Một người đứng cách chân ngọn hải đăng 50 m, nhìn xuống chân hải đăng dưới góc 2° và nhìn lên đỉnh ngọn hải đăng dưới góc 45° ...