Cho đường tròn (O) có bán kính bằng 2,5 cm và hai tia Ox, Oy vuông góc với nhau tại O

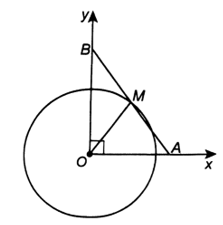
Cho đường tròn (O) có bán kính bằng 2,5 cm và hai tia Ox, Oy vuông góc với nhau tại O. Trên tia Ox lấy điểm A sao cho OA = 3 cm; trên tia Oy lấy điểm B sao cho OB = 4 cm. Gọi M là trung điểm của đoạn AB. Chứng minh rằng điểm M nằm trên đường tròn (O).

Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 13: Mở đầu về đường tròn - Kết nối tri thức

Bài 5.2 trang 56 sách bài tập Toán 9 Tập 1: Cho đường tròn (O) có bán kính bằng 2,5 cm và hai tia Ox, Oy vuông góc với nhau tại O. Trên tia Ox lấy điểm A sao cho OA = 3 cm; trên tia Oy lấy điểm B sao cho OB = 4 cm. Gọi M là trung điểm của đoạn AB. Chứng minh rằng điểm M nằm trên đường tròn (O).

Lời giải:

Áp dụng định lý Pythagore vào tam giác vuông AOB ta có:

$AB=\sqrt{O{A}^2+O{B}^2}=\sqrt{3^2+4^2}=5$ (cm)

M là trung điểm AB nên $OM=MA=MB=\frac{AB}{2}=\frac{5}{2}=\mathrm{2,5}$(cm)

Mà bán kính đường tròn (O) là 2,5 cm nên điểm M nằm trên đường tròn (O). (đpcm)

Lời giải SBT Toán 9 Bài 13: Mở đầu về đường tròn hay khác:

• Bài 5.1 trang 56 sách bài tập Toán 9 Tập 1: Các bánh xe (xe đạp, ô tô,...) đều có dạng hình tròn (với tâm tại trục của bánh xe). Hãy giải thích lí do ...

• Bài 5.3 trang 56 sách bài tập Toán 9 Tập 1: Trên mặt phẳng toạ độ Oxy, cho hai điểm A(0; –3) và B(2; 0). Gọi C và D là các điểm lần lượt đối xứng với A và B qua O ...

• Bài 5.4 trang 56 sách bài tập Toán 9 Tập 1: Trên mặt phẳng toạ độ Oxy, cho điểm A(3; 1). Gọi B, C và D là các điểm đối xứng với A lần lượt qua trục hoành, qua gốc O và qua trục tung ...

• Bài 5.5 trang 56 sách bài tập Toán 9 Tập 1: Cho đường tròn (O), đường kính AB và điểm M thuộc (O) (M không trùng với điểm nào trong hai điềm A và B) ...