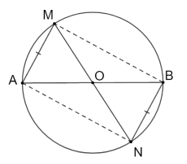
Cho đường tròn (O), đường kính AB và điểm M thuộc (O) M không trùng với điểm nào trong hai điềm A và B
Cho đường tròn (O), đường kính AB và điểm M thuộc (O) (M không trùng với điểm nào trong hai điềm A và B). Trên (O) lấy điểm N nằm khác phía của M đối với đường thẳng AB sao cho AM = BN. Chứng minh rằng O là trung điểm của đoạn MN.
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 13: Mở đầu về đường tròn - Kết nối tri thức
Bài 5.5 trang 56 sách bài tập Toán 9 Tập 1: Cho đường tròn (O), đường kính AB và điểm M thuộc (O) (M không trùng với điểm nào trong hai điềm A và B). Trên (O) lấy điểm N nằm khác phía của M đối với đường thẳng AB sao cho AM = BN. Chứng minh rằng O là trung điểm của đoạn MN.
Lời giải:
Xét ∆AOM và ∆BON có
Ta thấy: OM = ON (bán kính đường tròn (O))
OA = OB (bán kính đường tròn (O))
AM = BN (theo đề bài)
Do đó ∆AOM = ∆BON (c.c.c), suy ra
Ta có: (do A, O, B thẳng hàng).
Mà nên , suy ra ba điểm M, O, N thẳng hàng.
Mà OM = ON nên 3 điểm O là trung điểm của MN. (đpcm)
Lời giải SBT Toán 9 Bài 13: Mở đầu về đường tròn hay khác: