Hai túi I và II chứa các viên bi có cùng kích thước. Túi I chứa 4 viên bi được ghi các số 1, 2, 3, 4
Hai túi I và II chứa các viên bi có cùng kích thước. Túi I chứa 4 viên bi được ghi các số 1, 2, 3, 4. Túi II chứa 5 viên bi được ghi các số 1, 2, 3, 4, 5. Bạn Mai lấy ngẫu nhiên một viên bi từ túi I và bạn Tuấn lấy ngẫu nhiên một viên bi từ túi II. Tính xác suất của các biến cố sau:
Giải sách bài tập Toán 9 Bài 26: Xác suất của biến cố liên quan tới phép thử - Kết nối tri thức
Bài 8.10 trang 46 sách bài tập Toán 9 Tập 2: Hai túi I và II chứa các viên bi có cùng kích thước. Túi I chứa 4 viên bi được ghi các số 1, 2, 3, 4. Túi II chứa 5 viên bi được ghi các số 1, 2, 3, 4, 5. Bạn Mai lấy ngẫu nhiên một viên bi từ túi I và bạn Tuấn lấy ngẫu nhiên một viên bi từ túi II. Tính xác suất của các biến cố sau:
a) A: “Hai số ghi trên hai viên bi khác nhau”;
b) B: “Hai số ghi trên hai viên bi chênh nhau 1 đơn vị”;
c) C: “Hai số ghi trên hai viên bi chênh nhau 3 đơn vị”.
Lời giải:
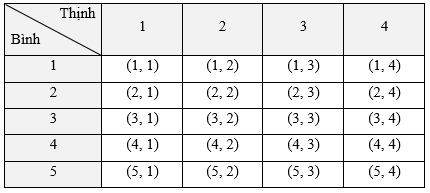
a) Bảng kết quả có thể xảy ra:
Không gian mẫu Ω = {(1, 1); (1, 2); (1, 3); …; (5, 3); (5, 4)}.
Ta có n(Ω) = 20.
Có 4 kết quả không thuận lợi cho biến cố A là (1, 1); (2, 2); (3, 3); (4; 4).
Vậy có 20 – 1 = 16 (kết quả thuận lợi cho biến cố A).
Vậy xác suất xảy ra của biến cố A là:
b) Có 7 kết quả thuận lợi cho biến cố B là (1, 2); (2, 1); (2, 3); (3, 2); (3, 4); (4, 3); (5, 4).
Vậy xác suất xảy ra của biến cố B là:
c) Có 7 kết quả thuận lợi cho biến cố C là (1, 4); (4, 1); (5, 2).
Vậy xác suất xảy ra của biến cố C là:
Lời giải SBT Toán 9 Bài 26: Xác suất của biến cố liên quan tới phép thử hay khác: