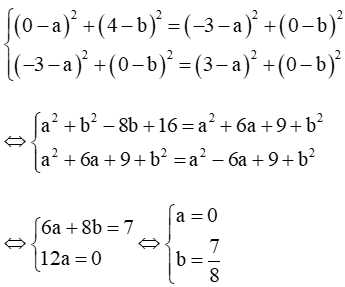Bài 11 trang 104 Toán lớp 10 Tập 2 Cánh diều

Cho tam giác AFF, trong đó A(0; 4), F(– 3; 0), F(3; 0).

Giải Toán lớp 10 Bài tập cuối chương 7

Bài 11 trang 104 Toán lớp 10 Tập 2: Cho tam giác AF₁F₂, trong đó A(0; 4), F₁(– 3; 0), F₂(3; 0).

a) Lập phương trình tổng quát của các đường thẳng AF₁ và AF₂.

b) Lập phương trình đường tròn ngoại tiếp của tam giác AF₁F₂.

c) Lập phương trình chính tắc của elip (E) có hai tiêu điểm là F₁, F₂ sao cho (E) đi qua A.

Lời giải:

a) Ta có: $\vec{A F_{1}} = (- 3; - 4)$ là một vectơ chỉ phương của đường thẳng AF₁, do đó đường thẳng này có một vectơ pháp tuyến là $\vec{n_{1}} = (4; - 3)$ .

Vậy phương trình tổng quát đường thẳng AF₁ là 4(x – 0) – 3(y – 4) = 0 hay 4x – 3y + 12 = 0.

Lại có: $\vec{A F_{2}} = (3; - 4)$ là một vectơ chỉ phương của đường thẳng AF₂, do đó đường thẳng này có một vectơ pháp tuyến là $\vec{n_{2}} = (4; 3)$ .

Vậy phương trình tổng quát đường thẳng AF₂ là 4(x – 0) + 3(y – 4) = 0 hay 4x + 3y – 12 = 0.

b) Đường tròn ngoại tiếp tam giác AF₁F₂ là đường tròn đi qua 3 điểm A, F₁, F₂.

Giả sử tâm của đường tròn là điểm I(a; b).

Ta có IA = IF₁ = IF₂ ⇔ IA² = $I F_{1}^{2}$ = $I F_{2}^{2}$ .

Vì IA² = $I F_{1}^{2}$ , $I F_{1}^{2}$ = $I F_{2}^{2}$ nên

Bài 11 trang 104 Toán lớp 10 Tập 2 Cánh diều

Đường tròn tâm $I (0; \frac{7}{8})$ bán kính R = IA = $\sqrt{{(0 - a)}^{2} + {(4 - b)}^{2}}$ $= \sqrt{{(4 - \frac{7}{8})}^{2}} = \frac{25}{8}$ .

Phương trình đường tròn (C) là ${(x - 0)}^{2} + {(y - \frac{7}{8})}^{2} = {(\frac{25}{8})}^{2}$ .

Vậy phương trình đường tròn (C) là $x^{2} + {(y - \frac{7}{8})}^{2} = \frac{625}{64}$ .

c) Phương trình chính tắc của elip (E) có dạng $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ .

Elip (E) đi qua điểm A(0; 4), thay tọa độ điểm A vào phương trình elip ta được $\frac{0^{2}}{a^{2}} + \frac{4^{2}}{b^{2}} = 1 \Leftrightarrow b^{2} = 4^{2} \Rightarrow b = 4 (d o b > 0)$ .

Elip (E) có hai tiêu điểm là F₁(– 3; 0), F₂(3; 0), do đó c = 3.

Suy ra a² – b² = c² hay a² – 4² = 3² ⇔ a² = 9 + 16 = 25 = 5², suy ra a = 5 (do a > 0).

Khi đó a > b > 0 (do 5 > 4 > 0), vậy a = 5, b = 4 là thỏa mãn.

Vậy phương trình elip (E) cần lập là $\frac{x^{2}}{5^{2}} + \frac{y^{2}}{4^{2}} = 1 h a y \frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ .

Lời giải Toán 10 Bài tập cuối chương 7 trang 103, 104 hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Giải Toán lớp 10 Cánh diều

Bài 11 trang 104 Toán lớp 10 Tập 2 Cánh diều

Giải Toán lớp 10 Bài tập cuối chương 7

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: