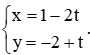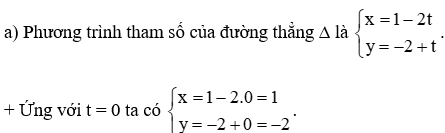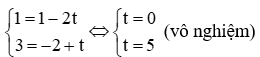Giải Toán 10 trang 75 Tập 2 Cánh diều

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 75 Tập 2 trong Bài 3: Phương trình đường thẳng Toán lớp 10 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 75.

Giải Toán 10 trang 75 Tập 2 Cánh diều

Luyện tập 1 trang 75 Toán lớp 10 Tập 2: Cho đường thẳng Δ có phương trình tham số

a) Chỉ ra tọa độ của hai điểm thuộc đường thẳng Δ.

b) Điểm nào trong các điểm C(– 1; – 1), D(1; 3) thuộc đường thẳng Δ.

Lời giải:

Điểm A(1; – 2) thuộc đường thẳng ∆.

+ Ứng với t = 1 ta có

Điểm B(– 1; – 1) thuộc đường thẳng ∆.

Chú ý: Ta chỉ cần lấy một số thực t bất kì thay vào phương trình tham số, ta sẽ được tọa độ 1 điểm thuộc đường thẳng ∆.

b) Theo câu a) điểm B(– 1; – 1) thuộc đường thẳng Δ ứng với t = 1, khi đó C ≡ B.

Vậy điểm C(– 1; – 1) thuộc đường thẳng ∆.

Thay tọa độ điểm D(1; 3) vào đường thẳng Δ ta được:

Vậy điểm D(1; 3) không thuộc đường thẳng ∆.

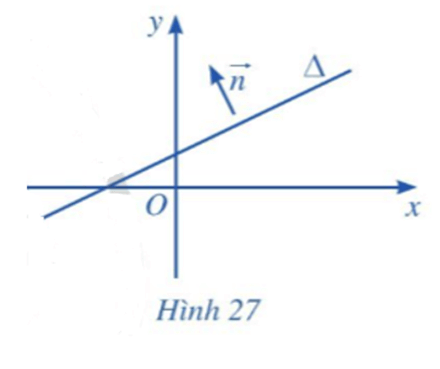
Hoạt động 3 trang 75 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆. Vẽ vectơ $\overrightarrow{n}\left(\overrightarrow{n}\ne \overrightarrow{0}\right)$ có giá vuông góc với đường thẳng ∆ (Hình 27).

Lời giải:

Cách vẽ:

- vẽ 1 đoạn thẳng vuông góc với đường thẳng ∆.

- Vẽ hướng mũi tên trên đoạn thẳng đó, ta được vectơ chỉ phương thỏa mãn yêu cầu bài toán.

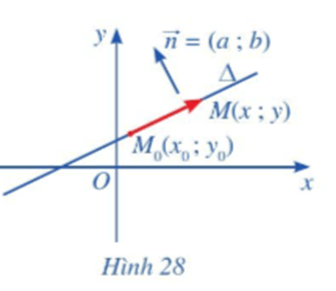
Hoạt động 4 trang 75 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ đi qua điểm M₀(x₀; y₀) và có vectơ pháp tuyến $\overrightarrow{n}=\left(a;b\right)$. Xét điểm M(x; y) nằm trên ∆ (Hình 28)

a) Nhận xét về phương của hai vectơ $\overrightarrow{n}$ và $\overrightarrow{M_{0}M}$.

b) Tìm mối liên hệ giữa tọa độ của điểm M với tọa độ của điểm M₀ và tọa độ của vectơ pháp tuyến $\overrightarrow{n}$.

Lời giải:

a) Vectơ $\overrightarrow{n}$ là vectơ pháp tuyến của đường thẳng ∆ nên giá của vectơ $\overrightarrow{n}$ vuông góc với đường thẳng ∆.

Đường thẳng ∆ đi qua điểm M₀ và M, nên đường thẳng ∆ chính là đường thẳng MM₀. Khi đó vectơ $\overrightarrow{M_{0}M}$ có giá chính là đường thẳng ∆.

Do đó giá của vectơ $\overrightarrow{n}$ và giá của vectơ $\overrightarrow{M_{0}M}$ vuông góc với nhau.

Vậy hai vectơ hai vectơ $\overrightarrow{n}$ và $\overrightarrow{M_{0}M}$ không cùng phương.

b) Ta có: $\overrightarrow{M_{0}M}=\left(x-x_0;y-y_0\right),\overrightarrow{n}=\left(a;b\right)$.

Xét điểm M(x; y) thuộc ∆. Vì $\overrightarrow{M_{0}M}\perp \overrightarrow{n}$ nên

$\overrightarrow{M_{0}M}.\overrightarrow{n}=0\iff$a(x – x₀) + b(y – y₀) = 0 ⇔ ax + by – ax₀ – by₀ = 0.

Lời giải bài tập Toán lớp 10 Bài 3: Phương trình đường thẳng Cánh diều hay khác:

• Giải Toán 10 trang 73 Tập 2
• Giải Toán 10 trang 74 Tập 2
• Giải Toán 10 trang 76 Tập 2
• Giải Toán 10 trang 79 Tập 2
• Giải Toán 10 trang 80 Tập 2