Giải Toán 10 trang 90 Tập 2 Cánh diều

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 90 Tập 2 trong Bài 5: Phương trình đường tròn Toán lớp 10 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 90.

Giải Toán 10 trang 90 Tập 2 Cánh diều

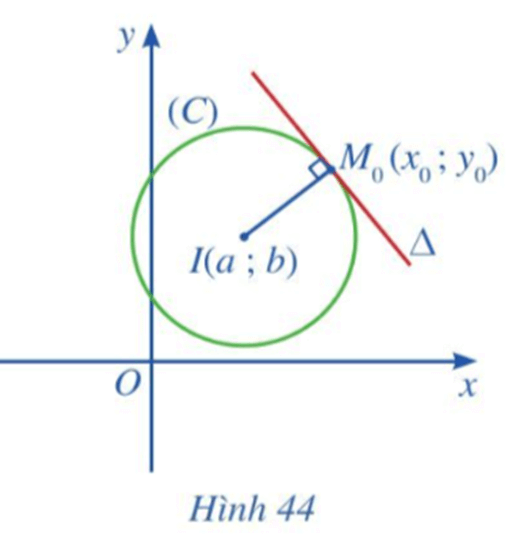
Hoạt động 4 trang 90 Toán lớp 10 Tập 2: Cho điểm M₀(x₀; y₀) nằm trên đường tròn (C) tâm I(a; b) bán kính R.

Gọi ∆ là tiếp tuyến tại điểm M₀(x₀; y₀) thuộc đường tròn (Hình 44).

a) Chứng tỏ rằng $\overrightarrow{I{M}_0}$ là vectơ pháp tuyến của đường thẳng ∆.

b) Tính tọa độ của $\overrightarrow{I{M}_0}$.

c) Lập phương trình tổng quát của đường thẳng ∆.

Lời giải:

a) Vì đường thẳng ∆ là tiếp tuyến của đường tròn (C) có tâm I tại điểm M₀ nên IM₀ vuông góc với ∆ tại M₀ (tiếp tuyến của đường tròn vuông góc với bán kính đi qua tiếp điểm).

Do đó, vectơ $\overrightarrow{I{M}_0}$ có giá là đường thẳng IM₀ vuông góc với đường thẳng ∆.

Vậy vectơ $\overrightarrow{I{M}_0}$ là vectơ pháp tuyến của đường thẳng ∆.

b) Ta có: $\overrightarrow{I{M}_0}=\left(x_0-a;y_0-b\right)$.

c) Đường thẳng ∆ đi qua điểm M₀(x₀; y₀) và nhận $\overrightarrow{I{M}_0}$ làm vectơ pháp tuyến.

Do đó, phương trình tổng quát của đường thẳng ∆ là(x₀ – a)(x – x₀) + (y₀ – b)(y – y₀) = 0.

Luyện tập 4 trang 90 Toán lớp 10 Tập 2: Lập phương trình tiếp tuyến tại điểm M₀(– 1; – 4) thuộc đường tròn (x – 3)² + (y + 7)² = 25.

Lời giải:

Đường tròn có tâm I(3; – 7).

Phương trình tiếp tuyến tại điểm M₀(– 1; – 4) thuộc đường tròn (x – 3)² + (y + 7)² = 25 là

(– 1 – 3)(x + 1) + (– 4 + 7)(y + 4) = 0

⇔ – 4x – 4 + 3y + 12 = 0 ⇔ 4x – 3y – 8 = 0.

Lời giải bài tập Toán lớp 10 Bài 5: Phương trình đường tròn Cánh diều hay khác:

• Giải Toán 10 trang 87 Tập 2
• Giải Toán 10 trang 88 Tập 2
• Giải Toán 10 trang 89 Tập 2
• Giải Toán 10 trang 91 Tập 2
• Giải Toán 10 trang 92 Tập 2