Giải Toán 11 trang 111 Tập 1 Chân trời sáng tạo
Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 111 Tập 1 trong Bài 3: Đường thẳng và mặt phẳng song song Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 111.
Giải Toán 11 trang 111 Tập 1 Chân trời sáng tạo
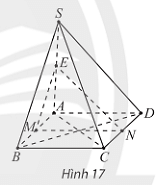
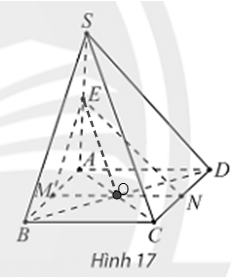
Thực hành 3 trang 111 Toán 11 Tập 1: Cho hình chóp S.ABC có ABCD là hình bình hành và M, N, E lần lượt là trung điểm của các đoạn thẳng AB, CD, SA (Hình 17). Chứng minh rằng:
a) MN song song với hai mặt phẳng (SBC) và (SAD);
b) SB và SC song song với mặt phẳng (MNE).
Lời giải:
a) Trong mặt phẳng (ABCD) có MN là đường trung bình của hình bình hành ABCD nên MN // BC// AD.
Ta có: MN // BC mà BC ⊂ (SBC) nên MN // (SBC).
Ta lại có: MN // AD mà AD ⊂ (SAD) nên MN // (SAD).
b)
Trong mặt phẳng (ABCD) gọi O là giao điểm của AC và BD, khi đó O là trung điểm của AC.
+) Xét tam giác SAC có E là trung điểm của SA, O là trung điểm của AC nên EO là đường trung bình của tam giác. Do đó EO // SC.
Mặt khác EO ⊂ (MNE) nên SC // (MNE).
+) Xét tam giác SAB có E là trung điểm của SA, M là trung điểm của AB nên EM là đường trung bình của tam giác. Do đó EM // SB.
Mặt khác EM ⊂ (MNE) nên SB // (MNE).
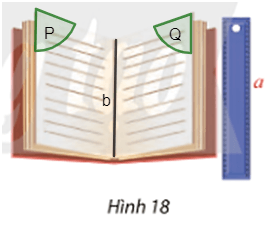
Vận dụng 2 trang 111 Toán 11 Tập 1: Làm thế nào để đặt cây thước kẻ a để nó song song với các trang của một cuốn sách?
Lời giải:
Gọi mỗi nửa sách là một mặt phẳng có tên lần lượt là (P) và (Q).
Đường thẳng b là giao điểm của hai mặt phẳng (P) và (Q).
Để đường thẳng a // (P) và a // (Q) thì a // b .
Vậy ta chỉ cần đặt thước kẻ a song song với lề sách thì a sẽ song song với các trang của cuốn sách.
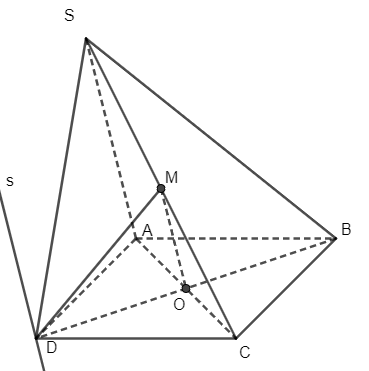
Bài 1 trang 111 Toán 11 Tập 1: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm hai đường chéo. Gọi M là trung điểm của SC.
a) Chứng minh đường thẳng OM song song với hai mặt phẳng (SAD) và (SBD).
b) Tìm giao tuyến của hai mặt phẳng (OMD) và (SAD).
Lời giải:
a) Trong mặt phẳng (SAC) có OM // SA mà SA ⊂ (SAD) nên OM // (SAD).
Mặt khác SA ⊂ (SAB) nên OM // (SAB).
b) Ta có: D ∈ (OMD) ∩ (SAD) mà OM // SA nên giao tuyến của hai mặt phẳng (OMD) và (SAD) là đường thẳng s đi qua D và song song với SA.
Lời giải bài tập Toán 11 Bài 3: Đường thẳng và mặt phẳng song song hay khác: