Giải Toán 11 trang 141 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 141 Tập 1 trong Bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 141.

Giải Toán 11 trang 141 Tập 1 Chân trời sáng tạo

Bài 2 trang 141 Toán 11 Tập 1: Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau:

a) Tìm tứ phân vị của dãy số liệu trên.

b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng tứ phân vị của mẫu số liệu từ bảng tần số ghép nhóm trên.

Lời giải:

a) Sắp xếp dãy số liệu theo thứ tự không giảm ta được:

6; 8; 8; 10; 11; 11; 12; 13; 14; 14; 14; 15; 18; 18; 21; 22; 23; 24; 25; 25.

Tứ phân vị thứ hai của mẫu số liệu là trung bình cộng của giá trị thứ 10 và thứ 11 ta được: $Q_2=\frac{14+14}{2}=14$.

Tứ phân vị thứ nhất là trung bình cộng của giá trị thứ 5 và thứ 6 ta được:

$Q_1=\frac{11+11}{2}=11$.

Tứ phân vị thứ ba là trung bình cộng của giá trị 15 và 16 ta được:

$Q_3=\frac{21+22}{2}=21,5$.

b) Ta có bảng tần số ghép nhóm theo mẫu sau:

Điểm số	[6; 10]	[11; 15]	[16; 20]	[21; 25]
Số trận	4	8	2	6

c) Ta có bảng hiểu chỉnh bảng trên như sau:

Điểm số	[5,5; 10,5)	[10,5; 15,5)	[15,5; 20,5)	[20,5; 25,5)
Số trận	4	8	2	6

Gọi x₁; x₂; ...; x₂₀ là lương tháng của nhân viên một văn phòng theo thứ tự không giảm.

Ta có: x₁; ...; x₄ ∈ [5,5; 10,5), x₅; ...; x₁₂ ∈ [10,5; 15,5), x₁₃; x₁₄ ∈ [15,5; 20,5), x₁₅; ...; x₂₀ ∈ [20,5; 25,5).

Khi đó:

- Tứ phân vị thứ hai của mẫu số liệu là trung bình cộng của x₁₀ và x₁₁. Vì x₁₀; x₁₁ ∈ [10,5; 15,5) nên Q₂ = $10,5+\frac{\frac{20}{2}-4}{8}(15,5-10,5)=14,25$.

- Tứ phân vị thứ nhất của mẫu số liệu là trung bình cộng của x₅ và x₆. Vì x₅; x₆ ∈ [10,5; 15,5) nên $Q_1=10,5+\frac{\frac{20}{4}-4}{8}(15,5-10,5)=11,125$.

- Tứ phân vị thứ ba của mẫu số liệu là trung bình cộng của x₁₅ và x₁₆. Vì x₁₅; x₁₆ ∈ [20,5; 25,5) nên $Q_3=20,5+\frac{\frac{3.20}{4}-14}{6}(25,5-20,5)\approx 21,3$.

Bài 3 trang 141 Toán 11 Tập 1: Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:

Hãy ước lượng số trung bình, mốt và tứ phân vị của mẫu số liệu ghép nhóm trên.

Lời giải:

Ta có bảng giá trị đại diện:

Điện lượng (nghìn mAh)	[0,9; 0,95)	[0,95; 1,0)	[1,0; 1,05)	[1,05; 1,1)	[1,1; 1,15)
Giá trị đại diện	0,925	0,975	1,025	1,075	1,125
Số viên pin	10	20	35	15	5

+) Ước lượng số trung bình của mẫu số liệu là:

$\overline{x}=\frac{0,925.10+0,975.20+1,025.35+1,075.15+1,125.5}{85}\approx 1,016$.

+) Mốt của dãy số liệu thuộc vào [1,0; 1,05) nên ta có: $M_0=1,0+\frac{35-20}{35-20+35-15}.(1,05-1,0)\approx 1,02$.

+) Gọi x₁; x₂; ...; x₈₅ là điện lượng của một số viên pin tiểu được sắp xếp theo thứ tự không giảm.

Ta có: x₁; ...; x₁₀ ∈ [0,9; 0,95), x₁₁; ...; x₃₀ ∈ [0,95; 1,0), x₃₁; ...; x₆₅ ∈ [1,0; 1,05), x₆₆; ...; x_80­ ∈ [1,05; 1,1), x₈₁; ...; x₈₅ ∈ [1,1; 1,15).

Khi đó, ta có:

- Tứ phân vị thứ hai của dãy số liệu là x₄₃ ∈ [1,0; 1,05) nên $Q_2=1,0+\frac{\frac{85}{2}-30}{35}.(1,05-1,0)\approx 1,02$.

- Tứ phân vị thứ nhất của dãy số liệu là $\frac{1}{2}$(x₂₁ + x₂₂) ∈ [0,95; 1,0) nên

$Q_1=0,95+\frac{\frac{85}{4}-10}{20}.(1,0-0,95)\approx 0,98$.

- Tứ phân vị thứ ba của dãy số liệu là $\frac{1}{2}$(x₆₃ + x₆₄) ∈ [1,0; 1,05) nên

$Q_3=1,0+\frac{\frac{3.85}{4}-30}{35}.(1,05-1,0)\approx 1,05$.

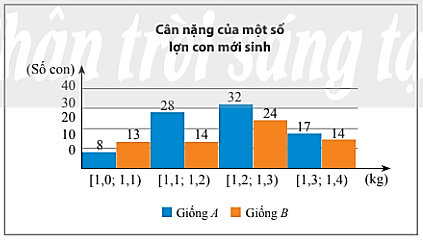
Bài 4 trang 141 Toán 11 Tập 1: Cân nặng của một số lợn con mới sinh thuộc hai giống A và B được cho ở biểu đồ dưới đây (đơn vị : kg).

a) Hãy so sánh cân nặng của lợn con mới sinh giống A và giống B theo số trung bình và trung vị.

b) Hãy ướng lượng tứ phân vị thứ nhất và thứ ba của cân nặng lợn con mới sinh giống A và cân nặng lợn con mới sinh giống B.

Lời giải:

a) Ta có bảng tần số ghép lớp như sau:

Cân nặng (kg)	[1,0; 1,1)	[1,1; 1,2)	[1,2; 1,3)	[1,3; 1,4)
Giá trị đại diện	1,05	1,15	1,25	1,35
Số con lợn giống A	8	28	32	17
Số con lợn giống B	13	14	24	14

+) Ước lượng cân nặng trung bình của lợn con giống A là:

$\overline{x_1}=\frac{1,05.8+1,15.28+1,25.32+1,35.17}{8+28+32+17}\approx 1,22$ (kg).

+) Ước lượng cân nặng trung bình của lợn con giống B là:

$\overline{x_2}=\frac{1,05.13+1,15.14+1,25.24+1,35.14}{13+14+24+14}\approx 1,21$ (kg).

Suy ra cân nặng trung bình của hai giống lợn con đều gần như nhau.

+) Tổng số lợn con giống A là 85 con.

Gọi x₁; ...; x₈₅ là cân nặng của một số lợn con mới sinh thuộc giống A theo thứ tự không giảm.

Ta có: x₁; ...; x₈ ∈ [1,0; 1,1), x₉; ...; x₃₆ ∈ [1,1; 1,2), x₃₇; ...; x₆₈ ∈ [1,2; 1,3), x₆₉; ...; x₈₅ ∈ [1,3; 1,4).

Tứ phân vị thứ hai của mẫu số liệu là giá trị x₄₃ ∈ [1,2; 1,3) nên

$Q_2=1,2+\frac{\frac{85}{2}-36}{32}.(1,3-1,2)\approx 1,22$ (kg).

- Tứ phân vị thứ nhất của mẫu số liệu là $\frac{1}{2}$(x₂₁ + x₂₂) và x₂₁, x₂₂ ∈ [1,1; 1,2) nên

$Q_1=1,1+\frac{\frac{85}{4}-8}{28}.(1,2-1,1)\approx 1,15$ (kg).

- Tứ phân vị thứ ba của mẫu số liệu là $\frac{1}{2}$(x₆₃ + x₆₄) và x₆₃; x₆₄ ∈ [1,2; 1,3) nên

$Q_3=1,2+\frac{\frac{3.85}{4}-36}{32}.(1,3-1,2)\approx 1,29$ (kg).

+) Tổng số lợn con giống B là 65 con.

Gọi y₁; ...; y₆₅ là cân nặng của một số lợn con mới sinh thuộc giống B theo thứ tự không giảm.

Ta có: y₁; ...; y₁₃ ∈ [1,0; 1,1), y₁₄; ...; y₂₇ ∈ [1,1; 1,2), y₂₈; ...; y₅₁ ∈ [1,2; 1,3), y₅₂; ...; y₆₅ ∈ [1,3; 1,4).

Tứ phân vị thứ hai của mẫu số liệu là giá trị y₃₃ ∈ [1,2; 1,3) nên

$Q_2=1,2+\frac{\frac{65}{2}-27}{24}.(1,3-1,2)\approx 1,22$ (kg).

- Tứ phân vị thứ nhất của mẫu số liệu là $\frac{1}{2}$(y₁₆ + y₁₇) và y₁₆, y₁₇ ∈ [1,1; 1,2) nên

$Q_1=1,1+\frac{\frac{65}{4}-13}{14}.(1,2-1,1)\approx 1,12$ (kg).

- Tứ phân vị thứ ba của mẫu số liệu là $\frac{1}{2}$(y₄₉ + x₅₀) và y₄₉; y₅₀ ∈ [1,2; 1,3) nên

$Q_3=1,2+\frac{\frac{3.65}{4}-27}{24}.(1,3-1,2)\approx 1,29$ (kg).

Lời giải bài tập Toán 11 Bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm hay khác:

• Giải Toán 11 trang 136

• Giải Toán 11 trang 137

• Giải Toán 11 trang 140