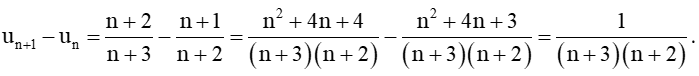Giải Toán 11 trang 61 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 61 Tập 1 trong Bài 3: Cấp số nhân Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 61.

Giải Toán 11 trang 61 Tập 1 Chân trời sáng tạo

Bài 7 trang 61 Toán 11 Tập 1: Giả sử một thành phố có dân số năm 2022 là khoảng 2,1 triệu người và tốc độ gia tăng dân số trung bình mỗi năm là 0,75%.

a) Dự đoán dân số của thành phố đó vào năm 2032.

b) Nếu tốc độ gia tăng dân số vẫn giữ nguyên như trên thì ước tính vào năm nào dân số của thành phố đó sẽ tăng gấp đôi so với năm 2022?

Lời giải:

Số dân của thành phố qua các năm với tốc độ gia tăng dân số trung bình mỗi năm là 0,75% lập thành một cấp số nhân (u_n) với số hạng đầu là u₁ = 2,1 (ở năm 2022) và công bội q = 1 + 0,75% = 1,0075 có số hạng tổng quát là: u_n = 2,1.(1,0075)^n-1.

a) Dự đoán dân số của thành phố vào năm 2032 là:

u₁₁ = 2,1.(1,0075)¹⁰ ≈ 2,3 triệu người.

b) Dân số của năm thứ n (so với năm 2022) là: 2.2,1 = 4,2 (triệu người).

Ta có: u_n = 2,1.(1,0075)^n-1 = 4,2

⇒ n – 1 ≈ 93

Vậy ước tính vào năm 2022 + 93 = 2115 thì dân số thành phố đó gấp đôi so với năm 2022.

Bài 8 trang 61 Toán 11 Tập 1: Trong trò chơi mạo hiểm nhảy bungee, mỗi lần nhảy, người chơi sẽ được dây an toàn có tính đàn hồi kéo nảy ngược lên 60% chiều sâu của cú nhảy. Một người chơi bungee thực hiện cú nhảy đầu tiên có độ cao nảy ngược lên là 9m.

a) Tính độ cao nảy ngược lên của người đó ở lần nảy thứ ba.

b) Tính tổng các độ cao nảy ngược lên của người đó trong 5 lần nảy đầu.

Lời giải:

Độ cao nảy ngược lên của người chơi bungee sau mỗi lần thực hiện cú nhảy lập thành một cấp số nhân có số hạng đầu tiên u₁ = 9 và công bội q = 0,06.

Suy ra số hạng tổng quát của cấp số nhân là: u_n = 9.(0,06)^n-1.

a) Độ cao nảy ngược lên của người đó ở lần thứ 3 là:

u₃ = 9.(0,06)² = 1,994.10^-3 (m).

b) Tổng các độ cao nảy ngược lên của người đó trong 5 lần nảy đầu là tổng 5 số hạng đầu của cấp số nhân và bằng: $S_5=\frac{9.\left(1-0,{06}^5\right)}{1-0,06}\approx 9,6$.

Bài 1 trang 61 Toán 11 Tập 1: Cho dãy số (u­_n) với u_n = $\frac{n}{3^n-1}$. Ba số hạng đầu tiên của dãy số (u_n) lần lượt là

A. $\frac{1}{2};\frac{1}{4};\frac{3}{27}$;

B. $\frac{1}{2};\frac{1}{4};\frac{3}{26}$;

C. $\frac{1}{2};\frac{1}{4};\frac{3}{25}$;

D. $\frac{1}{2};\frac{1}{4};\frac{3}{28}$.

Lời giải:

Đáp án đúng là: B

Dãy số (u­_n) có ba số hạng đầu tiên là:

$u_1=\frac{1}{3^1-1}=\frac{1}{2}$;

$u_2=\frac{2}{3^2-1}=\frac{2}{8}=\frac{1}{4}$;

$u_3=\frac{3}{3^3-1}=\frac{3}{26}$

Bài 2 trang 61 Toán 11 Tập 1: Cho dãy số $\frac{1}{3};\frac{1}{3^2};\frac{1}{3^3};\frac{1}{3^4};\frac{1}{3^5};\mathrm{...}$. Số hạng tổng quát của dãy số này là:

A. $u_n=\frac{1}{3}.\frac{1}{3^{n+1}}$;

B. $u_n=\frac{1}{3^{n+1}}$;

C. $u_n=\frac{1}{3^n}$;

D. $u_n=\frac{1}{3^{n-1}}$.

Lời giải:

Đáp án đúng là: C

Dãy số $\frac{1}{3};\frac{1}{3^2};\frac{1}{3^3};\frac{1}{3^4};\frac{1}{3^5};\mathrm{...}$ lập thành một cấp số nhân có số hạng đầu là $\frac{1}{3}$ và công bội q = $\frac{1}{3}$, có số hạng tổng quát là: $u_n=\frac{1}{3}.{\left(\frac{1}{3}\right)}^{n-1}={\left(\frac{1}{3}\right)}^n$.

Bài 3 trang 61 Toán 11 Tập 1: Cho dãy số (u­_n) với $u_n=\frac{n+1}{n+2}$. Phát biểu nào sau đây là đúng?

A. Dãy số tăng và bị chặn;

B. Dãy số giảm và bị chặn;

C. Dãy số giảm và bị chặn dưới;

D. Dãy số giảm và bị chặn trên.

Lời giải:

Đáp án đúng là: A

+) Ta có: $u_{n+1}=\frac{n+1+1}{n+1+2}=\frac{n+2}{n+3}$

Xét hiệu

Vì n ∈ ℕ^* nên n > 0, suy ra $\frac{1}{\left(n+3\right)\left(n+2\right)}>0$.

Do đó u_n+1 > u_n hay (u_n) là dãy tăng.

+) Ta có: $u_n=1-\frac{1}{n+2}$

Vì n ∈ ℕ^* nên n ≥ 1 suy ra n + 2 ≥ 3

$\Rightarrow u_n=1-\frac{1}{n+2}\ge 1-\frac{1}{3}=\frac{2}{3},\forall n\in {\mathbb{N}}^{*}$.

Ta lại có n ∈ ℕ^* nên n > 0 suy ra $\frac{1}{n+2}>0$. Do đó $u_n=1-\frac{1}{n+2}<1$.

Vì vậy $\frac{2}{3}\le u_n<1$ nên dãy số (u_n) bị chặn.

Bài 4 trang 61 Toán 11 Tập 1: Cho cấp số cộng (u­_n) có số hạng đầu u₁, công sai d. Khi đó, với n ≥ 2 ta có

A. u_n = u₁ + d;

B. u_n = u₁ + (n + 1)d;

C. u_n = u₁ – (n – 1)d;

D. u_n = u₁ + (n – 1)d.

Lời giải:

Đáp án đúng là: D

Cấp số cộng (u­_n) có số hạng đầu u₁, công sai d có số hạng tổng quát là:

u_n = u₁ + (n – 1)d, với n ≥ 2.

Bài 5 trang 61 Toán 11 Tập 1: Cho cấp số cộng (u­_n) có u₁ = 3 và u₂ = – 1. Khi đó

A. u₃ = 4;

B. u₃ = 2;

C. u₃ = – 5;

D. u₃ = 7.

Lời giải:

Đáp án đúng là: C

Ta có: u₂ = u₁ + d = – 1

⇔ d = – 1 – u₁ = – 1 – 3 = – 4.

Khi đó u₃ = u₁ + 2d = 3 + 2(– 4) = – 5.

Lời giải bài tập Toán 11 Bài 3: Cấp số nhân Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 57

• Giải Toán 11 trang 58

• Giải Toán 11 trang 59

• Giải Toán 11 trang 60