Bài 2.32 trang 57 Toán 11 Tập 1 - Kết nối tri thức

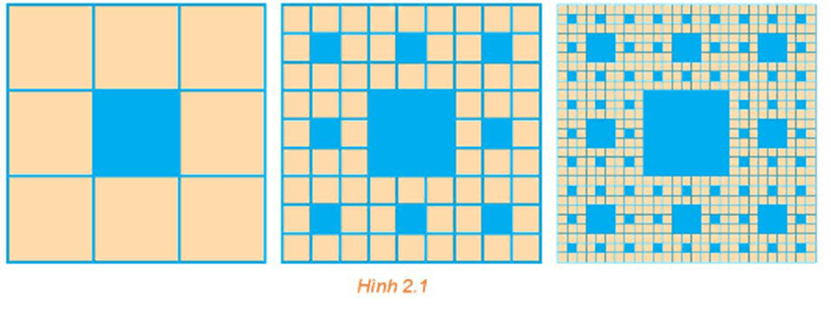
Một hình vuông màu vàng có cạnh 1 đơn vị dài được chia thành chín hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh như Hình 2.1. Mỗi hình vuông màu vàng nhỏ hơn lại được chia thành chín hình vuông con, và mỗi hình vuông con ở chính giữa là được tô màu xanh. Nếu quá trình này được tiếp tục lặp lại năm lần, thì tổng diện tích các hình vuông được tô màu xanh bằng bao nhiêu?

Giải Toán 11 Bài tập cuối chương 2 - Kết nối tri thức

Bài 2.32 trang 57 Toán 11 Tập 1: Một hình vuông màu vàng có cạnh 1 đơn vị dài được chia thành chín hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh như Hình 2.1. Mỗi hình vuông màu vàng nhỏ hơn lại được chia thành chín hình vuông con, và mỗi hình vuông con ở chính giữa là được tô màu xanh. Nếu quá trình này được tiếp tục lặp lại năm lần, thì tổng diện tích các hình vuông được tô màu xanh bằng bao nhiêu?

Lời giải:

+ Chia lần 1: Hình vuông màu vàng lớn có cạnh bằng 1 đơn vị thì có diện tích bằng 1 (đvdt). Chia hình vuông này thành 9 hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh, thì hình vuông màu xanh đầu tiên này có diện tích bằng $\frac{1}{9}$ (đvdt).

+ Chia lần 2: 8 hình vuông màu vàng còn lại, mỗi hình vuông này lại được chia thành 9 hình vuông con và tiếp tục tô xanh hình vuông chính giữa, khi đó mỗi hình vuông xanh nhỏ hơn có diện tích S₁ = $\frac{1}{9}\cdot \frac{1}{9}=\frac{1}{9^2}$, 8 hình vuông xanh nhỏ hơn có diện tích bằng 8S₁.

Cứ tiếp tục như vậy, mỗi lần chia ta sẽ tạo thành 8 hình vuông xanh nhỏ hơn tiếp đối với mỗi ô vuông vàng nhỏ.

Do đó, quá trình này được tiếp tục lặp lại năm lần, thì trừ lần đầu tiên, 4 lần sau, mỗi lần chia diện tích ô vuông xanh tạo thành lập thành một cấp số nhân có u₁ = $8.\frac{1}{9^2}$ và công bội $q=8.\frac{1}{9}$.

Vậy tổng diện tích các hình vuông được tô màu xanh là

S = $\frac{1}{9}+\frac{8.\frac{1}{9^2}\left(1-{\left(\frac{8}{9}\right)}^4\right)}{1-\frac{8}{9}}=\frac{26281}{59049}$ (đvdt).

Lời giải bài tập Toán 11 Bài tập cuối chương 2 hay, chi tiết khác:

• Bài 2.22 trang 56 Toán 11 Tập 1: Khẳng định nào sau đây là sai? ....

• Bài 2.23 trang 56 Toán 11 Tập 1: Cho dãy số 1, $\frac{1}{2},\frac{1}{4},\frac{1}{8},\mathrm{...}$ ....

• Bài 2.24 trang 56 Toán 11 Tập 1: Cho dãy số (u_n) với u_n = 3n + 6. Khẳng định nào sau đây là đúng? ....

• Bài 2.25 trang 56 Toán 11 Tập 1: Trong các dãy số cho bởi công thức truy hồi sau, dãy số nào là cấp số nhân? ....

• Bài 2.26 trang 56 Toán 11 Tập 1: Tổng 100 số hạng đầu của dãy số (u_n) với u_­n = 2n – 1 là ....

• Bài 2.27 trang 57 Toán 11 Tập 1: Từ 0 giờ đến 12 giờ trưa, chuông của một chiếc đồng hồ quả lắc sẽ đánh bao nhiêu tiếng ....

• Bài 2.28 trang 57 Toán 11 Tập 1: Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần ....

• Bài 2.29 trang 57 Toán 11 Tập 1: Chứng minh rằng: a) Trong một cấp số cộng (u_n), mỗi số hạng (trừ số hạng đầu và số hạng cuối, nếu có) đều là trung bình cộng ....

• Bài 2.30 trang 57 Toán 11 Tập 1: Tìm ba số, biết theo thứ tự chúng lập thành cấp số cộng và có tổng bằng 21 ....

• Bài 2.31 trang 57 Toán 11 Tập 1: Mặt sàn tầng một (tầng trệt) của một ngôi nhà cao hơn mặt sân 0,5 m ....