Bài 4.17 trang 87 Toán 11 Tập 1 - Kết nối tri thức
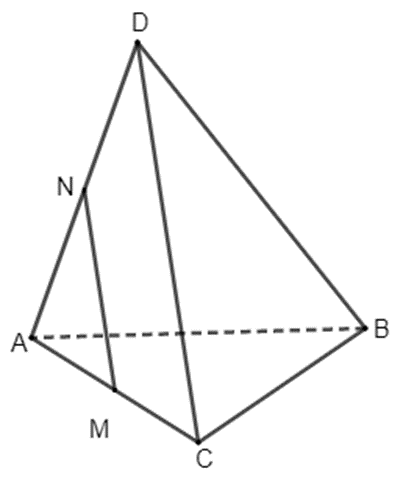
Cho hai tam giác ABC và ABD không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trung điểm của các cạnh AC, AD.
Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức
Bài 4.17 trang 87 Toán 11 Tập 1: Cho hai tam giác ABC và ABD không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trung điểm của các cạnh AC, AD.
a) Đường thẳng AM có song song với mặt phẳng (BCD) hay không? Hãy giải thích tại sao.
b) Đường thẳng MN có song song với mặt phẳng (BCD) hay không? Hãy giải thích tại sao.
Lời giải:
a) Vì M là trung điểm của cạnh AC nên đường thẳng AM chứa điểm C.
Lại có điểm C thuộc mặt phẳng (BCD) và điểm A không thuộc mặt phẳng (BCD) (do bốn điểm A, B, C, D không đồng phẳng). Do đó, đường thẳng AM cắt mặt phẳng (BCD) tại điểm C. Vậy đường thẳng AM không song song với mặt phẳng (BCD).
b) Vì M, N lần lượt là trung điểm của các cạnh AC, AD nên MN là đường trung bình của tam giác ACD, suy ra MN // CD.
Lại có đường thẳng CD nằm trong mặt phẳng (BCD) và đường thẳng MN không nằm trong mặt phẳng (BCD).
Vậy đường thẳng MN song song với mặt phẳng (BCD).
Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác: