c) Cho AB = a, BC = b, CC' = c. Tính AC'.
Câu hỏi:
c) Cho AB = a, BC = b, CC' = c. Tính AC'.
Trả lời:
c) Vì ABCD là hình chữ nhật nên .
Vì CC' ^ (ABCD) nên CC' ^ AC.
Xét tam giác C'CA vuông tại C, có .
Vậy .
Câu hỏi:
c) Cho AB = a, BC = b, CC' = c. Tính AC'.
Trả lời:
c) Vì ABCD là hình chữ nhật nên .
Vì CC' ^ (ABCD) nên CC' ^ AC.
Xét tam giác C'CA vuông tại C, có .
Vậy .
Câu 1:
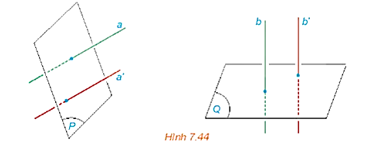
Cho hai mặt phẳng (P) và (Q). Lấy hai đường thẳng a, a' cùng vuông góc với (P), hai đường thẳng b, b' cùng vuông góc với (Q). Tìm mối quan hệ giữa các góc (a, b) và (a', b').
Câu 3:
Cho hình chóp S.ABCD, đáy ABCD là một hình chữ nhật có tâm O, SO ^ (ABCD). Chứng minh rằng hai mặt phẳng (SAC) và (SBD) vuông góc với nhau khi và chỉ khi ABCD là một hình vuông.
Câu 4:
Cho mặt phẳng (P) chứa đường thẳng b vuông góc với mặt phẳng (Q). Lấy một đường thẳng a vuông góc với (P). (H.7.47).
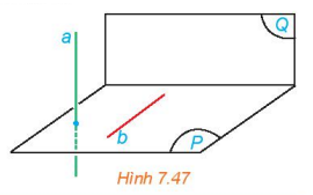
a) Tính góc giữa a và b.
b) Tính góc giữa (P) và (Q).
Câu 5:
Cho hình chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b.
a) Tính sin của góc tạo bởi cạnh bên và mặt đáy.
Câu 7:
Hai mái nhà trong Hình 7.72 là hai hình chữ nhật. Giả sử AB = 4,8 m; OA = 2,8 m; OB = 4 m.
a) Tính (gần đúng) số đo của góc nhị diện tạo bởi hai nửa mặt phẳng tương ứng chứa hai mái nhà.
Câu 8:
b) Chứng minh rằng mặt phẳng (OAB) vuông góc với mặt đất phẳng. Lưu ý: Đường giao giữa hai mái (đường nóc) song song với mặt đất.
