Cho khối chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích của khối chóp.
Câu hỏi:
Cho khối chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích của khối chóp.
Trả lời:
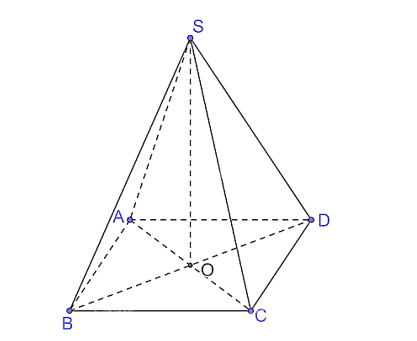
Gọi O là giao điểm của AC và BD. Vì S.ABCD là hình chóp đều nên SO ^ (ABCD).
Xét tam giác BCD vuông tại C, có BD=√BC2+CD2=√a2+a2=a√2 .
Vì ABCD là hình vuông nên O là trung điểm của BD, suy ra BO=BD2=a√22 .
Xét tam giác SOB vuông tại O, có SO=√SB2−OB2=√b2−a22 .
Ta có . VS.ABCD=13⋅SABCD⋅SO=13⋅a2⋅√b2−a22=13⋅a2⋅√2b2−a22 .
