Một sọt đựng đồ có dạng hình chóp cụt đều (H.7.98). Đáy và miệng sọt là các hình vuông tương ứng có cạnh bằng 30 cm, 60 cm, cạnh bên của sọt dài 50 cm. Tính thể tích của sọt.
Câu hỏi:
Một sọt đựng đồ có dạng hình chóp cụt đều (H.7.98). Đáy và miệng sọt là các hình vuông tương ứng có cạnh bằng 30 cm, 60 cm, cạnh bên của sọt dài 50 cm. Tính thể tích của sọt.

Trả lời:
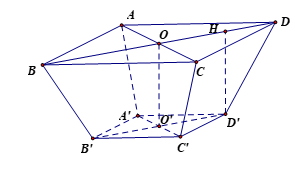
Sọt đựng đồ có dạng hình chóp cụt đều ABCD.A'B'C'D'.
Ta có S1 = SABCD = 602 = 3 600(cm2), S2 = SA'B'C'D' = 302 = 900 (cm2).
Kẻ D'H ^ BD tại H.
Gọi O và O' lần lượt là tâm của hình vuông ABCD và A'B'C'D'.
Vì OO' ^ (ABCD) nên OO' ^ OH, OO' ^ (A'B'C'D') nên OO' ^ B'D'.
Do đó OHD'O' là hình chữ nhật, suy ra O'D' = OH, OO' = HD'.
Xét tam giác B'C'D' vuông tại C', có
(cm).
Vì O' là trung điểm của B'D' nên (cm).
Xét tam giác BCD vuông tại C, có
(cm).
Mà O là trung điểm của BD nên (cm).
Có HD = DO – OH = (cm).
Xét tam giác DHD' vuông tại H, có
(cm).
Do đó (cm).
(cm3).