Câu hỏi:
Cho tứ diện ABCD có .
a) Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc với BC.
Trả lời:
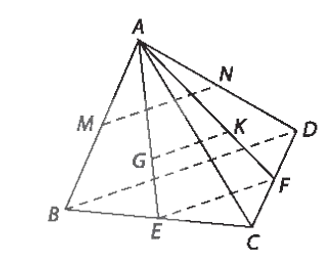
a) Xét tam giác ABD, có M là trung điểm của AB, N là trung điểm của AD nên MN là đường trung bình của tam giác ABD, suy ra MN // BD.
Khi đó (MN, BC) = (BD, BC) = .
Vậy MN vuông góc với BC.
Câu 1:
Đối với các nút giao thông cùng mức hay khác mức, để có thể dễ dàng bố trí các nhánh rẽ và để người tham gia giao thông có góc nhìn đảm bảo an toàn, khi thiết kế người ta đều cố gắng để các tuyến đường tạo với nhau một góc đủ lớn và tốt nhất là góc vuông. Đối với nút giao thông cùng mức, tức là các đường giao nhau, thì góc giữa chúng là góc giữa hai đường thẳng mà ta đã biết. Còn đối với các nút giao khác mức, tức là các đường thẳng chéo nhau, thì góc giữa chúng được hiểu như thế nào? Bài học này sẽ đề cập tới đối tượng toán học tương ứng.
Câu 2:
Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O, O' tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a', b' tương ứng song song với m, n (H.7.2).
a) Mỗi cặp đường thẳng a, a' và b, b' có cùng thuộc một mặt phẳng hay không?
b) Lấy các điểm A, B (khác O) tương ứng thuộc a, b. Đường thẳng qua A song song với OO' cắt a' tại A', đường thẳng qua B song song với OO' cắt b' tại B'. Giải thích vì sao OAA'O'; OBB'O'; ABB'A' là các hình bình hành.
Câu 3:
c) So sánh góc giữa hai đường thẳng a, b và góc giữa hai đường thẳng a', b'.
(Gợi ý: Áp dụng định lí côsin cho các tam giác OAB, O'A'B' ).
Câu 4:
Nếu a song song hoặc trùng với a' và b song song hoặc trùng với b' thì (a, b) và (a', b') có mối quan hệ gì?
Câu 5:
b) Gọi G, K tương ứng là trọng tâm của các tam giác ABC, ACD. Chứng minh rằng GK vuông góc với BC.
Câu 6:
Đối với nhà gỗ truyền thống, trong các cấu kiện: hoành, quá giang, xà cái, rui, cột tương ứng được đánh số 1, 2, 3, 4, 5 như trong Hình 7.8, những cặp cấu kiện nào vuông góc với nhau?
