Hoàn thành bảng sau: Số đo độ 15° ? 0° 900° ? ? Số đo rađian
Câu hỏi:
Hoàn thành bảng sau:
|
Số đo độ
|
15°
|
?
|
0°
|
900°
|
?
|
?
|
|
Số đo rađian
|
?
|
\(\frac{{3\pi }}{8}\)
|
?
|
?
|
\( - \frac{{7\pi }}{{12}}\)
|
\( - \frac{{11\pi }}{8}\)
|
Trả lời:
Lời giải:
Để hoàn thành bảng đã cho, ta thực hiện chuyển đổi từ độ sang rađian và từ rađian sang độ.
Ta có: 15° = 15 . \(\frac{\pi }{{180}}\) = \(\frac{\pi }{{12}}\);
0° = 0 . \(\frac{\pi }{{180}}\) = 0;
900° = 900 . \(\frac{\pi }{{180}}\) = 5π;
\(\frac{{3\pi }}{8} = \frac{{3\pi }}{8} \cdot \left( {\frac{{180}}{\pi }} \right)\begin{array}{*{20}{c}}^\circ \\{}\end{array} = 67,5^\circ \);
\( - \frac{{7\pi }}{{12}} = - \frac{{7\pi }}{{12}} \cdot \left( {\frac{{180}}{\pi }} \right)\begin{array}{*{20}{c}}^\circ \\{}\end{array} = - 105^\circ \);
\( - \frac{{11\pi }}{8} = - \frac{{11\pi }}{8} \cdot \left( {\frac{{180}}{\pi }} \right)\begin{array}{*{20}{c}}^\circ \\{}\end{array} = - 247,5^\circ \).
Vậy ta hoàn thành được bảng như sau:
|
Số đo độ
|
15°
|
67,5°
|
0°
|
900°
|
– 105°
|
– 247,5°
|
|
Số đo rađian
|
\(\frac{\pi }{{12}}\)
|
\(\frac{{3\pi }}{8}\)
|
0
|
5π
|
\( - \frac{{7\pi }}{{12}}\)
|
\( - \frac{{11\pi }}{8}\)
|
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết:
Câu 1:
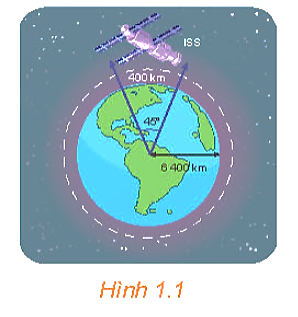
Trạm vũ trụ Quốc tế ISS (tên Tiếng Anh: International Space Station) nằm trong quỹ đạo tròn cách bề mặt Trái Đất khoảng 400 km (H.1.1). Nếu trạm mặt đất theo dõi được trạm vũ trụ ISS khi nó nằm trong góc 45° ở tâm của quỹ đạo tròn này phía trên ăng-ten theo dõi, thì trạm vũ trụ ISS đã di chuyển được bao nhiêu kilômét trong khi nó đang được trạm mặt đất theo dõi? Giả sử rằng bán kính của Trái Đất là 6 400 km. Làm tròn kết quả đến hàng đơn vị.
Xem lời giải »
Câu 2:
Trên đồng hồ ở Hình 1.2, kim phút đang chỉ đúng số 2.

a) Phải quay kim phút mấy phần của một vòng tròn theo chiều quay ngược chiều kim đồng hồ để nó chỉ đúng số 12?
b) Phải quay kim phút mấy phần của một vòng tròn theo chiều quay của chiều kim đồng hồ để nó chỉ đúng số 12?
c) Có bao nhiêu cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12?
Xem lời giải »
Câu 3:
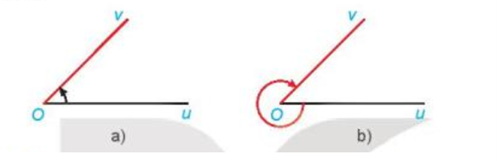
Cho góc hình học \(\widehat {uOv}\) = 45°. Xác định số đo của góc lượng giác (Ou, Ov) trong mỗi trường hợp sau:
Xem lời giải »
Câu 4:
Cho ba tia Ou, Ov, Ow với số đo của các góc hình học uOv và vOw lần lượt là 30° và 45°.
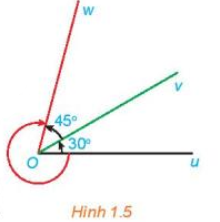
a) Xác định số đo của ba góc lượng giác (Ou, Ov), (Ov, Ow) và (Ou, Ow) được chỉ ra ở Hình 1.5.
b) Với các góc lượng giác ở câu a, chứng tỏ rằng có một số nguyên k để
sđ(Ou, Ov) + sđ(Ov, Ow) = sđ(Ou, Ow) + k360°.
Xem lời giải »
Câu 5:
Một đường tròn có bán kính 20 cm. Tìm độ dài của các cung trên đường tròn đó có số đo sau:
a) \(\frac{\pi }{{12}}\);
b) 1,5;
c) 35°;
d) 315°.
Xem lời giải »
Câu 6:
Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau:
a) \(\frac{{2\pi }}{3}\);
b) \( - \frac{{11\pi }}{4}\);
c) 150°;
d) – 225°.
Xem lời giải »
Câu 7:
Tính các giá trị lượng giác của góc α, biết:
a) cos α = \(\frac{1}{5}\) và 0 < α < \(\frac{\pi }{2}\);
b) sin α = \(\frac{2}{3}\) và \(\frac{\pi }{2} < \alpha < \pi \);
c) tan α = \(\sqrt 5 \) và \(\pi < \alpha < \frac{{3\pi }}{2}\);
d) cot α = \( - \frac{1}{{\sqrt 2 }}\) và \(\frac{{3\pi }}{2} < \alpha < 2\pi \).
Xem lời giải »
Câu 8:
Chứng minh các đẳng thức:
a) cos4 α – sin4 α = 2cos2 α – 1;
b) \(\frac{{{{\cos }^2}\alpha + {{\tan }^2}\alpha - 1}}{{{{\sin }^2}\alpha }} = {\tan ^2}\alpha \).
Xem lời giải »