Tính đạo hàm f'(x0) tại điểm x0 bất kì trong các trường hợp sau: b) f(x) = x.

Nếu một quả bóng được thả rơi tự do từ đài quan sát trên sân thượng của tòa nhà Landmark 81 (Thành phố Hồ Chí Minh) cao 461,3 m xuống mặt đất. Có tính được vận tốc của quả bóng khi nó chạm đất hay không? (Bỏ qua sức cản không khí).

Một vật di chuyển trên một đường thẳng (H.9.2). Quãng đường s của chuyển động là một hàm số của thời gian t, s = s(t) (được gọi là phương trình của chuyển động).

a) Tính vận tốc trung bình của vật trong khoảng thời gian từ t₀ đến t.

b) Giới hạn $\underset{t\to t_0}{\lim }\frac{s\left(t\right)-s\left(t_0\right)}{t-t_0}$  cho ta biết điều gì ?

Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t, có dạng Q = Q(t).

a) Tính cường độ trung bình của dòng điện trong khoảng thời gian từ t₀ đến t.

Tính đạo hàm f'(x₀) tại điểm x₀ bất kì trong các trường hợp sau:

a) y = x² + 1

Tính đạo hàm f'(x₀) tại điểm x₀ bất kì trong các trường hợp sau:

b) y = kx + c (với k, c là các hằng số).

Nhận biết tiếp tuyến của đồ thị hàm số

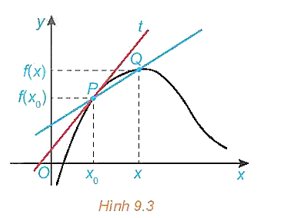
Cho hàm số y = f(x) có đồ thị (C) và P(x₀; f(x₀)) ∈ (C). Xét điểm Q(x; f(x)) thay đổi trên (C) với x ≠ x₀.

a) Đường thẳng đi qua hai điểm P, Q được gọi là một cát tuyến của đồ thị (C) (H.9.3). Tìm hệ số góc k_PQ của cát tuyến PQ.

b) Khi x → x₀ thì vị trí của điểm Q(x; f(x)) trên đồ thị (C) thay đổi như thế nào ?