Giải Toán 11 trang 81 Tập 1 Kết nối tri thức
Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 81 Tập 1 trong Bài 11: Hai đường thẳng song song Toán lớp 11 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 81.
Giải Toán 11 trang 81 Tập 1 Kết nối tri thức
Luyện tập 3 trang 81 Toán 11 Tập 1: Trong Ví dụ 1, chứng minh rằng bốn điểm C, D, E, F đồng phẳng và tứ giác CDFE là hình bình hành.
Lời giải:
Ta có: EF // AB (do ABEF là hình bình hành) và CD // AB (do ABCD là hình bình hành).
Do đó, CD // EF.
Khi đó, hai đường thẳng CD và EF đồng phẳng hay bốn điểm C, D, E, F đồng phẳng.
Lại có EF = AB và CD = AB (do ABEF và ABCD là các hình bình hành) nên CD = EF.
Vậy tứ giác CDFE là hình bình hành.
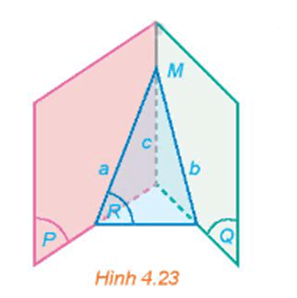
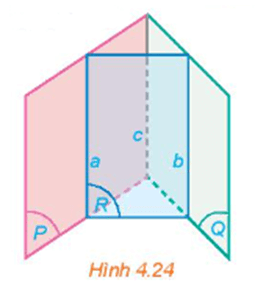
HĐ4 trang 81 Toán 11 Tập 1: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến c. Một mặt phẳng (R) cắt (P) và (Q) lần lượt theo các giao tuyến a và b khác c.
a) Nếu hai đường thẳng a và c cắt nhau tại M thì đường thẳng b có đi qua M hay không (H.4.23)? Giải thích vì sao.
b) Nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c có song song với nhau hay không (H.4.24)? Giải thích vì sao.
Lời giải:
a) Vì M thuộc a nằm trong mặt phẳng (R) nên M thuộc mặt phẳng (R).
Vì M thuộc c nằm trong mặt phẳng (Q) nên M thuộc mặt phẳng (Q).
Do đó, M là một điểm chung của hai mặt phẳng (R) và (Q).
Lại có hai mặt phẳng (R) và (Q) có giao tuyến là đường thẳng b.
Vậy M thuộc b hay đường thẳng b đi qua điểm M.
b) Ta thấy ba đường thẳng phân biệt a, b, c đôi một đồng phẳng.
Do đó, nếu không có hai trong ba đường thẳng nào trong chúng cắt nhau thì a, b, c đôi một song song.
Vậy nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c song song với nhau.
Lời giải bài tập Toán 11 Bài 11: Hai đường thẳng song song Kết nối tri thức hay khác: