Giải Toán 11 trang 90 Tập 1 Kết nối tri thức
Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 90 Tập 1 trong Bài 13: Hai mặt phẳng song song Toán lớp 11 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 90.
Giải Toán 11 trang 90 Tập 1 Kết nối tri thức
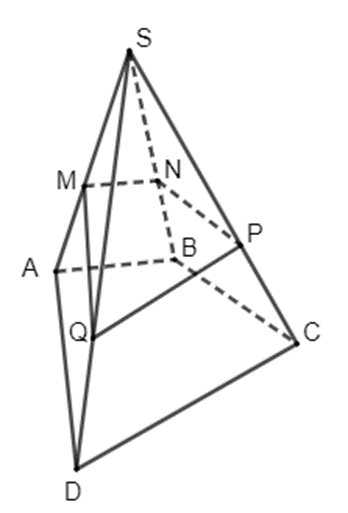
Luyện tập 2 trang 90 Toán 11 Tập 1: Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là các điểm thuộc cạnh SA, SB, SC, SD sao cho . Chứng minh rằng bốn điểm M, N, P, Q đồng phẳng.
Lời giải:
Xét tam giác SAB có hay , suy ra MN // AB (theo định lí Thalés). Do đó MN song song với mặt phẳng (ABCD). Tương tự, NP // BC nên NP song song với mặt phẳng (ABCD). Vậy mặt phẳng (MNP) chứa hai đường thẳng cắt nhau MN và NP cùng song song với mặt phẳng (ABCD) nên mặt phẳng (MNP) song song với mặt phẳng (ABCD). Lập lập tương tự ta có mặt phẳng (MPQ) cũng song song với mặt phẳng (ABCD).
Hai mặt phẳng (MNP) và (MPQ) cùng đi qua điểm M và cùng song song với mặt phẳng (ABCD) nên hai mặt phẳng đó trùng nhau, tức là bốn điểm M, N, P, Q đồng phẳng.
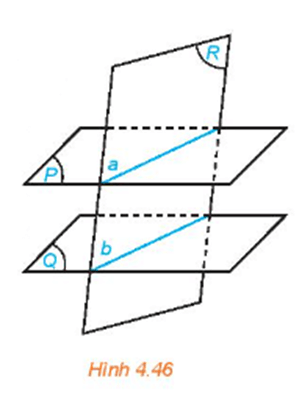
HĐ4 trang 90 Toán 11 Tập 1: Cho hai mặt phẳng song song (P) và (Q). Giả sử mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a (H.4.46).
a) Giải thích vì sao mặt phẳng (R) cắt mặt phẳng (Q).
b) Gọi b là giao tuyến của hai mặt phẳng (R) và (Q). Hai đường thẳng a và b có thể chéo nhau hay không, có thể cắt nhau hay không?
Lời giải:
a) Giả sử mặt phẳng (R) không cắt mặt phẳng (Q), tức là hai mặt phẳng (R) và (Q) song song với nhau, mà mặt phẳng (P) song song với mặt phẳng (Q), do đó mặt phẳng (R) cũng song song với mặt phẳng (P) (hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau), mẫu thuẫn với giả thiết (R) cắt (P) theo giao tuyến a.
Vậy mặt phẳng (R) cắt mặt phẳng (Q).
b) Vì a và b cùng thuộc mặt phẳng (R) nên hai đường thẳng a và b không thể chéo nhau.
Hai đường thẳng a và b không có điểm chung, vì nếu chúng có điểm chung A thì hai mặt phẳng (P) và (Q) cũng có điểm chung A (mâu thuẫn với giả thiết (P) và (Q) song song với nhau). Vậy hai đường thẳng a và b không thể cắt nhau.
Lời giải bài tập Toán 11 Bài 13: Hai mặt phẳng song song Kết nối tri thức hay khác: