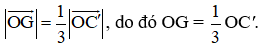Bài 13 trang 83 Toán 12 Tập 1 Cánh diều
Giải Toán 12 Bài tập cuối chương 2 - Cánh diều
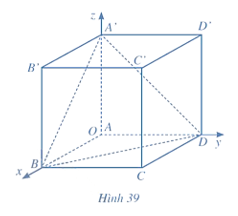
Bài 13 trang 83 Toán 12 Tập 1: Xét hệ toạ độ Oxyz gắn với hình lập phương ABCD.A'B'C'D' như Hình 39, đơn vị của mỗi trục bằng độ dài cạnh hình lập phương. Biết A(0; 0; 0), B(1; 0; 0), D(0; 1; 0), A'(0; 0; 1).
a) Xác định toạ độ các đỉnh còn lại của hình lập phương ABCD.A'B'C'D'.
b) Xác định toạ độ trọng tâm G của tam giác A'BD.
c) Xác định toạ độ các vectơ và . Chứng minh rằng ba điểm O, G, C' thẳng hàng và OG = OC'.
Lời giải:
a) Ta có điểm C thuộc mặt phẳng (Oxy) nên cao độ của điểm C bằng 0.
Lại có CB ⊥ Ox tại B nên hoành độ của điểm C là 1, CD ⊥ Oy tại D nên tung độ của điểm C là 1. Vậy C(1; 1; 0).
Tương tự như vậy, ta xác định được B'(1; 0; 1) và D'(0; 1; 1).
Ta có .
Áp dụng quy tắc hình hộp trong hình lập phương ABCD.A'B'C'D' ta có
= (0+1+0; 0+0+1; 1+0+0) = (1;1;1)
Do đó, , suy ra C'(1; 1; 1).
b) Gọi tọa độ trọng tâm G của tam giác A'BD là (xG; yG; zG).
Ta có .
Vậy .
c) Vì nên
Ta có , do đó .
Suy ra hai vectơ và cùng phương nên hai hai đường OG và OC' song song hoặc trùng nhau, mà OG ∩ OC' = O nên hai đường thẳng này trùng nhau, tức là ba điểm O, G, C' thẳng hàng.
Từ suy ra ,
Lời giải bài tập Toán 12 Bài tập cuối chương 2 hay, chi tiết khác:
Bài 1 trang 82 Toán 12 Tập 1: Cho điểm M thỏa mãn . Tọa độ của điểm M là: ....
Bài 2 trang 82 Toán 12 Tập 1: Cho hai điểm M(1; – 2; 3) và N(3; 4; – 5). Tọa độ của vectơ là: ....
Bài 3 trang 82 Toán 12 Tập 1: Cho hai vectơ ,. Tọa độ của vectơ là: ....
Bài 4 trang 82 Toán 12 Tập 1: Cho hai vectơ . Tọa độ của vectơ là: ....
Bài 5 trang 82 Toán 12 Tập 1: Cho vectơ . Tọa độ của vectơ là: ....
Bài 7 trang 82 Toán 12 Tập 1: Tích vô hướng của hai vectơ và là: ....