Hoạt động khám phá 9 trang 55 Toán 12 Tập 2 Chân trời sáng tạo

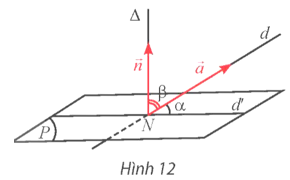
Cho đường thẳng d có vectơ chỉ phương và mặt phẳng (P) có vectơ pháp tuyến . Biết d cắt (P) tại điểm N và hình chiếu vuông góc của d lên (P) là đường thẳng d'. Qua N vẽ đường thẳng ∆ vuông góc với (P) (Hình 12).

Giải Toán 12 Bài 2: Phương trình đường thẳng trong không gian - Chân trời sáng tạo

Hoạt động khám phá 9 trang 55 Toán 12 Tập 2: Cho đường thẳng d có vectơ chỉ phương $\overrightarrow{a}=\left(a_1;a_2;a_3\right)$ và mặt phẳng (P) có vectơ pháp tuyến $\overrightarrow{n}=\left(n_1;n_2;n_3\right)$. Biết d cắt (P) tại điểm N và hình chiếu vuông góc của d lên (P) là đường thẳng d'. Qua N vẽ đường thẳng ∆ vuông góc với (P) (Hình 12).

a) Nhắc lại định nghĩa góc giữa đường thẳng và mặt phẳng trong không gian.

b) Có nhận xét gì về số đo của hai góc α = (d, d'); β = (∆, d)?

c) Giải thích tại sao ta lại có đẳng thức: $\sin \left(d,\left(P\right)\right)=\left|\cos \left(\overrightarrow{a},\overrightarrow{n}\right)\right|$

Lời giải:

a) Nếu đường thẳng a không vuông góc với (P) thì góc giữa a và hình chiếu a' của a trên (P) gọi là góc giữa đường thẳng a và (P). Kí hiệu (a, (P)).

b) Ta có α + β = 90° hay (d, d') + (∆, d) = 90° => (d, d') = 90° − (∆, d).

c) Vì (d, (P)) = (d, d') = 90° − (∆, d).

Do đó sin(d, (P)) = sin(90° − (∆, d)) = cos(∆, d) = $\left|\cos \left(\overrightarrow{a},\overrightarrow{n}\right)\right|$

Lời giải bài tập Toán 12 Bài 2: Phương trình đường thẳng trong không gian hay, chi tiết khác:

• Hoạt động khởi động trang 43 Toán 12 Tập 2: Ta đã biết trong mặt phẳng Oxy, phương trình tham số của đường thẳng có dạng: $\left\{\begin{array}{l}x=x_0+a_{1}t\\ y=y_0+a_{2}t\end{array}\right.\left(a_1^2+a_2^2\ne \mathrm{0,}t\in ℝ\right)$ ....

• Hoạt động khám phá 1 trang 44 Toán 12 Tập 2: Trong không gian Oxyz, cho điểm M₀ cố định và vectơ $\overrightarrow{a}$ khác $\overrightarrow{0}$ ....

• Thực hành 1 trang 44 Toán 12 Tập 2: Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A'B'C' với A(1; 2; 1), B(7; 5; 3), C(4; 2; 0), A'(4; 9; 9) ....

• Hoạt động khám phá 2 trang 44 Toán 12 Tập 2: Trong không gian Oxyz, cho đường thẳng d đi qua điểm M0(x0; y0; z0) cố định và có vectơ chỉ phương ....

• Thực hành 2 trang 46 Toán 12 Tập 2: Cho đường thẳng d có phương trình tham số $\left\{\begin{array}{l}x=-1+8t\\ y=-4t\\ z=3+12t\end{array}\right.$ ....

• Thực hành 3 trang 46 Toán 12 Tập 2: Viết phương trình tham số của đường thẳng d đi qua điểm A(5; 0; −7) và nhận $\overrightarrow{v}=\left(9;0;-2\right)$ ....

• Hoạt động khám phá 3 trang 46 Toán 12 Tập 2: Cho đường thẳng d có phương trình tham số $\left\{\begin{array}{l}x=x_0+a_{1}t\\ y=y_0+a_{2}t\\ z=z_0+a_{3}t\end{array}\right.$ với a₁, a₂, a₃ đều khác 0 ....

• Thực hành 4 trang 46 Toán 12 Tập 2: Viết phương trình chính tắc của đường thẳng d đi qua điểm M₀(5; 0; −6) và nhận $\overrightarrow{a}=\left(3;2;-4\right)$ làm vectơ chỉ phương ....

• Hoạt động khám phá 4 trang 47 Toán 12 Tập 2: Cho đường thẳng d đi qua hai điểm A(2; 2; 1) và B(4; 5; 3) ....

• Thực hành 5 trang 47 Toán 12 Tập 2: Viết phương trình tham số và phương trình chính tắc của đường thẳng MN, biết M(2; 0; −1) và N(4; 3; 1 ....

• Vận dụng 1 trang 47 Toán 12 Tập 2: Một mô hình cầu treo được thiết kế trong không gian Oxyz như Hình 4 ....

• Hoạt động khám phá 5 trang 48 Toán 12 Tập 2: Cho ba đường thẳng $d:\left\{\begin{array}{l}x=4+t\\ y=1+2t\\ z=1+3t\end{array}\right.$; $d^{\text{'}}:\left\{\begin{array}{l}x=2t^{\text{'}}\\ y=7+4t^{\text{'}}\\ z=2+6t^{\text{'}}\end{array}\right.$ và $d^{\text{'}\text{'}}:\left\{\begin{array}{l}x=5+2t^{\text{'}\text{'}}\\ y=3+4t^{\text{'}\text{'}}\\ z=4+6t^{\text{'}\text{'}}\end{array}\right.$ ....

• Thực hành 6 trang 49 Toán 12 Tập 2: Kiểm tra tính song song hoặc trùng nhau của các cặp đường thẳng sau ....

• Vận dụng 2 trang 49 Toán 12 Tập 2: Trên một máy khoan bàn đã thiết lập sẵn một hệ tọa độ. Nêu nhận xét về vị trí giữa trục d của mũi khoan ....

• Hoạt động khám phá 6 trang 50 Toán 12 Tập 2: Cho ba đường thẳng $d:\left\{\begin{array}{l}x=1+t\\ y=2+3t\\ z=3-t\end{array}\right.$; $d^{\text{'}\text{'}}:\left\{\begin{array}{l}x=2-2t^{\text{'}}\\ y=-2+t^{\text{'}}\\ z=1+3t^{\text{'}}\end{array}\right.$ và $d^{\text{'}\text{'}}:\left\{\begin{array}{l}x=2-2t^{\text{'}\text{'}}\\ y=-2+t^{\text{'}\text{'}}\\ z=3+3t^{\text{'}\text{'}}\end{array}\right.$ ....

• Thực hành 7 trang 52 Toán 12 Tập 2: Xét vị trí tương đối giữa hai đường thẳng d và d' trong mỗi trường hợp sau ....

• Vận dụng 3 trang 52 Toán 12 Tập 2: Trên phần mềm thiết kế chiếc cầu treo, cho đường thẳng d trên trụ cầu và đường thẳng d' trên sàn cầu có phương trình ....

• Hoạt động khám phá 7 trang 52 Toán 12 Tập 2: Cho hai đường thẳng d: $\left\{\begin{array}{l}x=4+t\\ y=1+2t\\ z=1-t\end{array}\right.$ và $d^{\text{'}}:\left\{\begin{array}{l}x=t^{\text{'}}\\ y=7+4t^{\text{'}}\\ z=9t^{\text{'}}\end{array}\right.$ ....

• Thực hành 8 trang 53 Toán 12 Tập 2: Kiểm tra tính vuông góc của các cặp đường thẳng sau ....

• Vận dụng 4 trang 53 Toán 12 Tập 2: Một phần mềm mô phỏng vận động viên đang tập bắn súng trong không gian Oxyz ....

• Hoạt động khám phá 8 trang 53 Toán 12 Tập 2: Cho hai đường thẳng d và d' có vectơ chỉ phương lần lượt là $\overrightarrow{a}=\left(2;1;3\right)$, $\overrightarrow{a^{\text{'}}}=\left(3;2;-8\right)$ ....

• Thực hành 9 trang 55 Toán 12 Tập 2: Tính góc giữa hai đường thẳng d và d' trong mỗi trường hợp sau ....

• Vận dụng 5 trang 55 Toán 12 Tập 2: Trên một phần mềm đã thiết kế sân khấu 3D trong không gian Oxyz. Tính góc giữa hai tia sáng có phương trình ....

• Thực hành 10 trang 56 Toán 12 Tập 2: Tính góc giữa đường thẳng d và mặt phẳng (P) trong mỗi trường hợp sau ....

• Vận dụng 6 trang 56 Toán 12 Tập 2: Trên một sân khấu đã thiết lập sẵn một hệ tọa độ Oxyz ....

• Hoạt động khám phá 10 trang 57 Toán 12 Tập 2: Cho hai mặt phẳng (P) và (P') có vectơ pháp tuyến lần lượt là $\overrightarrow{n}=\left(n_1;n_2;n_3\right),\overrightarrow{n^{\text{'}}}=\left({n^{\text{'}}}_1;{n^{\text{'}}}_2;{n^{\text{'}}}_3\right)$ (Hình 14) ....

• Thực hành 11 trang 58 Toán 12 Tập 2: Tính góc giữa hai mặt phẳng (P) và (P') trong mỗi trường hợp sau ....

• Thực hành 12 trang 59 Toán 12 Tập 2: Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A'B'C'D'. Cho biết A(0; 0; 0), B(1; 0; 0), D(0; 5; 0), A'(0; 0; 3) ....

• Vận dụng 7 trang 59 Toán 12 Tập 2: Để làm thí nghiệm về chuyển động trong mặt phẳng nghiêng, người làm thí nghiệm đã thiết lập sẵn một hệ tọa độ Oxyz ....

• Bài 1 trang 59 Toán 12 Tập 2: Viết phương trình tham số của đường thẳng a trong mỗi trường hợp sau ....

• Bài 2 trang 59 Toán 12 Tập 2: Viết phương trình chính tắc của đường thẳng b trong mỗi trường hợp sau ....

• Bài 3 trang 59 Toán 12 Tập 2: Cho đường thẳng d có phương trình chính tắc $\frac{x-3}{1}=\frac{y+3}{3}=\frac{z-2}{7}$ ....

• Bài 4 trang 59 Toán 12 Tập 2: Trong trò chơi mô phỏng bắn súng 3D trong không gian Oxyz, một xạ thủ đang ngắm với tọa độ khe ngắm và đầu ruồi lần lượt ....

• Bài 5 trang 60 Toán 12 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau: a) $d:\left\{\begin{array}{l}x=1+t\\ y=-1+2t\\ z=-2+t\end{array}\right.$ và $d^{\text{'}}:\left\{\begin{array}{l}x=2+2t^{\text{'}}\\ y=3+4t^{\text{'}}\\ z=2t^{\text{'}}\end{array}\right.$ ....

• Bài 6 trang 60 Toán 12 Tập 2: Viết phương trình tham số của đường thẳng d đi qua điểm A(1; 0; 1) và song song với đường thẳng d':$\frac{x+1}{3}=\frac{y-1}{2}=\frac{z-1}{4}$ ....

• Bài 7 trang 60 Toán 12 Tập 2: Trên phần mềm mô phỏng 3D một máy khoan trong không gian Oxyz, cho biết phương trình trục a của mũi khoan và một đường rãnh b ....

• Bài 8 trang 60 Toán 12 Tập 2: Tính góc giữa hai đường thẳng $d:\frac{x-3}{2}=\frac{y+5}{4}=\frac{z-7}{2}$ và $d^{\text{'}}:\frac{x-1}{3}=\frac{y+7}{3}=\frac{z-12}{6}$ ....

• Bài 9 trang 60 Toán 12 Tập 2: Tính góc giữa đường thẳng d: $\frac{x+2}{2}=\frac{y+2}{2}=\frac{z-1}{1}$ và mặt phẳng (P): 3y – 3z + 1 = 0 ....

• Bài 10 trang 60 Toán 12 Tập 2: Tính góc giữa hai mặt phẳng (P): 4y + 4z + 1 = 0 và (P'): 7x + 7z + 2 = 0 ....

• Bài 11 trang 60 Toán 12 Tập 2: Trên một cánh đồng điện mặt trời, người ta đã thiết lập sẵn một hệ tọa độ Oxyz ....

• Bài 12 trang 60 Toán 12 Tập 2: Trong không gian Oxyz, cho hình lăng trụ đứng OBC.O'B'C' có đáy là tam giác OBC vuông tại O ....