Giải Toán 12 trang 65 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 12 trang 65 Tập 1 trong Bài tập cuối chương 2 Toán 12 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 65.

Giải Toán 12 trang 65 Tập 1 Chân trời sáng tạo

Bài 1 trang 65 Toán 12 Tập 1: Cho điểm M thỏa mãn $\overrightarrow{OM}=2\overrightarrow{i}+\overrightarrow{j}$. Tọa độ của điểm M là:

A. M(0; 2; 1).

B. M(1; 2; 0).

C. M(2; 0; 1).

D. M(2; 1; 0).

Lời giải:

Đáp án đúng là: D

Vì $\overrightarrow{OM}=2\overrightarrow{i}+\overrightarrow{j}$ nên $M\left(2;1;0\right)$ .

Bài 2 trang 65 Toán 12 Tập 1: Cho hai điểm A(−1; 2; −3) và B(2; −1; 0). Tọa độ của vectơ $\overrightarrow{AB}$ là

A. $\overrightarrow{AB}=\left(1;-1;1\right)$ .

B. $\overrightarrow{AB}=\left(3;3;-3\right)$ .

C. $\overrightarrow{AB}=\left(1;1;-3\right)$ .

D. $\overrightarrow{AB}=\left(3;-3;3\right)$ .

Lời giải:

Đáp án đúng là: D

Ta có $\overrightarrow{AB}=\left(2+1;-1-2;0+3\right)=\left(3;-3;3\right)$

Bài 3 trang 65 Toán 12 Tập 1: Cho hai điểm A(3; −2; 3) và B(−1; 2; 5). Tọa độ trung điểm I của đoạn thẳng AB là

A. I(−2; 2; 1).

B. I(1; 0; 4).

C. I(2; 0; 8).

D. I(2; −2; −1).

Lời giải:

Đáp án đúng là: B

Tọa độ trung điểm I là

$I\left(\frac{3-1}{2};\frac{-2+2}{2};\frac{3+5}{2}\right)$ hay I(1;0;4) .

Bài 4 trang 65 Toán 12 Tập 1: Cho ba điểm A(1; 3; 5), B(2; 0; 1), C(0; 9; 0). Tọa độ trọng tâm G của tam giác ABC là

A. G(3; 12; 6).

B. G(1; 5; 2).

C. G(1; 0; 5).

D. G(1; 4; 2).

Lời giải:

Đáp án đúng là: D

Tọa độ trung điểm G là

$G\left(\frac{1+2+0}{3};\frac{3+0+9}{3};\frac{5+1+0}{3}\right)$hay G(1;4;2).

Bài 5 trang 65 Toán 12 Tập 1: Cho A(1; 2; −1), B(2; 1; −3), C(−3; 5; 1). Điểm D sao cho ABCD là hình bình hành có tọa độ là

A. D(−4; 6; 3).

B. D(−2; 2; 5).

C. D(−2; 8; −3).

D. D(−4; 6; −5).

Lời giải:

Đáp án đúng là: A

ABCD là hình bình hành $\iff \overrightarrow{AB}=\overrightarrow{DC}$ $\iff \left\{\begin{array}{l}2-1=-3-x_D\\ 1-2=5-y_D\\ -3+1=1-z_D\end{array}\right.$$\iff \left\{\begin{array}{l}{x}_D=-4\\ y_D=6\\ z_D=3\end{array}\right.$

Vậy D(−4; 6; 3).

Bài 6 trang 65 Toán 12 Tập 1: Gọi α là góc giữa hai vectơ $\overrightarrow{u}=\left(0;-1;0\right)$ và $\overrightarrow{v}=\left(\sqrt{3};1;0\right)$. Giá trị của α là

A. $\alpha =\frac{\pi }{6}$ .

B. $\alpha =\frac{\pi }{3}$ .

C. $\alpha =\frac{2\pi }{3}$ .

D. $\alpha =\frac{\pi }{2}$ .

Lời giải:

Đáp án đúng là: C

Ta có $\cos \alpha =\frac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}=\frac{0.\sqrt{3}+\left(-1\right).1+0.0}{\sqrt{{\left(-1\right)}^2}.\sqrt{3+1}}=-\frac{1}{2}$

Bài 7 trang 65 Toán 12 Tập 1: Cho A(2; −1; 1), B(−1; 3; −1), C(5; −3; 4). Tích vô hướng $\overrightarrow{AB}.\overrightarrow{BC}$ có giá trị là

A. 48.

B. −48.

C. 52.

D. −52.

Lời giải:

Đáp án đúng là: D

Có $\overrightarrow{AB}=\left(-3;4;-2\right)$ , $\overrightarrow{BC}=\left(6;-6;5\right)$ .

Có $\overrightarrow{AB}.\overrightarrow{BC}=\left(-3\right).6+4.\left(-6\right)+\left(-2\right).5=-52$ .

Bài 8 trang 65 Toán 12 Tập 1: Cho hai điểm A(−1; 2; 3), B(1; 0; 2). Tọa độ điểm M thỏa mãn $\overrightarrow{AB}=2\overrightarrow{MA}$ là

A. $M\left(-2;3;\frac{7}{2}\right)$ .

B. $M\left(-2;-3;\frac{7}{2}\right)$ .

C. M(−2; 3; 7).

D. M(−4; 6; 7).

Lời giải:

Đáp án đúng là: A

Giả sử M(x; y; z).

Có $\overrightarrow{AB}=\left(2;-2;-1\right)$ và $\overrightarrow{MA}=\left(-1-x;2-y;3-z\right)$ .

Vì $\overrightarrow{AB}=2\overrightarrow{MA}$  nên $\left\{\begin{array}{l}2=2\left(-1-x\right)\\ -2=2\left(2-y\right)\\ -1=2\left(3-z\right)\end{array}\right.$ $\iff \left\{\begin{array}{l}x=-2\\ y=3\\ z=\frac{7}{2}\end{array}\right.$. Vậy $M\left(-2;3;\frac{7}{2}\right)$ .

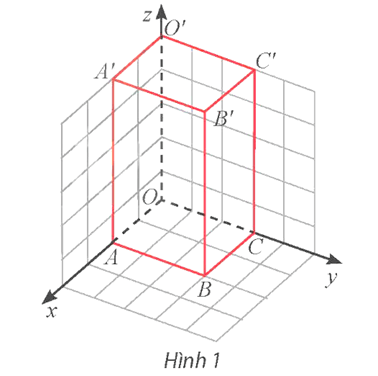
Bài 9 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, cho hình hộp chữ nhật OABC.O'A'B'C' như Hình 1, biết B'(2; 3; 5).

a) Tìm tọa độ các đỉnh còn lại của hình hộp.

b) Tính độ dài đường chéo OB' của hình hộp chữ nhật đó.

Lời giải:

a) Dựa vào Hình 1 ta có:

O(0; 0; 0), A(2; 0; 0), B(2; 3; 0), C(0; 3; 0),

O'(0; 0; 5), A'(2; 0; 5), B'(2; 3; 5), C'(0; 3; 5).

b) Có $O{B}^{\text{'}}=\sqrt{2^2+3^2+5^2}=\sqrt{38}$ .

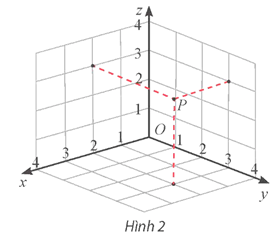
Bài 10 trang 65 Toán 12 Tập 1: Tìm tọa độ của điểm P được biểu diễn trong Hình 2 và tính khoảng cách OP.

Lời giải:

Ta có P(2; 3; 3).

Khi đó $OP=\sqrt{2^2+3^2+3^2}=\sqrt{22}$ .

Lời giải bài tập Toán 12 Bài tập cuối chương 2 hay khác:

• Giải Toán 12 trang 66