Giải Toán 12 trang 89 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 12 trang 89 Tập 1 trong Bài 1: Vẽ đồ thị hàm số bằng phần mềm Geogebra Toán 12 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 89.

Giải Toán 12 trang 89 Tập 1 Chân trời sáng tạo

Thực hành 1 trang 89 Toán 12 Tập 1: Vẽ đồ thị các hàm số bậc ba sau:

a) y = x³;       b) y = x³ – 3x;

c) y = −x³ + 3x;    d) y = x³ – 3x + 2.

Lời giải:

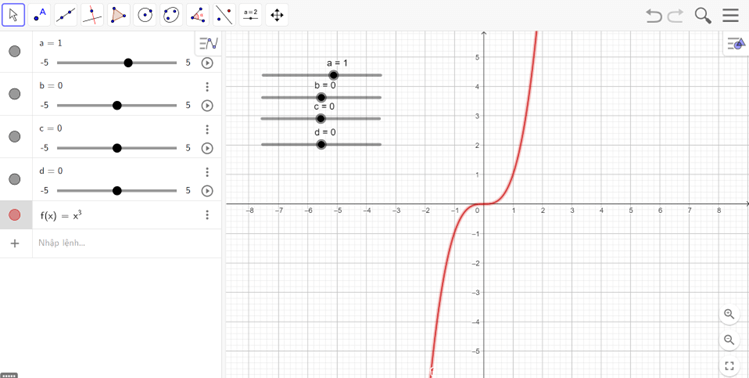
a) y = x³

- Tạo các thanh trượt biểu thị các tham số a, b, c, d bằng cách nhấp chuột liên tiếp vào thanh công cụ và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

- Nhập hàm số y = x³ vào vùng nhập lệnh.

- Ta được đồ thị như hình vẽ

- Nhận xét:

Hàm số đồng biến trên khoảng (0; +∞) và nghịch biến trên khoảng (−∞; 0).

Hàm số đã cho không có cực trị.

Đồ thị có tâm đối xứng là (0; 0).

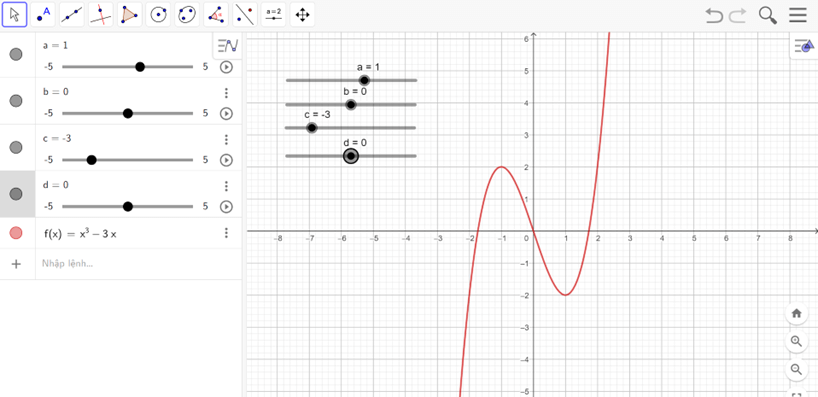
b) y = x³ – 3x

- Tạo các thanh trượt biểu thị các tham số a, b, c, d bằng cách nhấp chuột liên tiếp vào thanh công cụ và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

- Nhập hàm số y = x³ – 3x vào vùng nhập lệnh.

- Ta được đồ thị như hình vẽ

Nhận xét:

Hàm số đồng biến trên các khoảng (−∞; −1) và (1; +∞).

Hàm số nghịch biến trên khoảng (−1; 1).

Điểm cực đại là (−1; 2), điểm cực tiểu là (1; −2).

Đồ thị hàm số có tâm đối xứng là (0; 0).

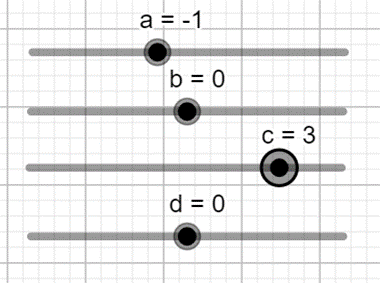
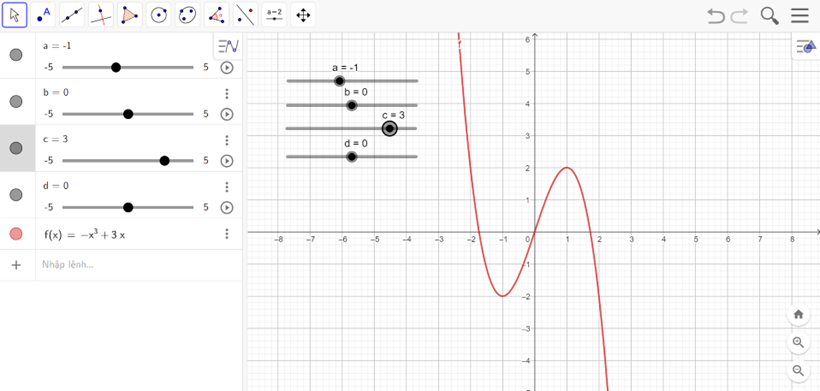
c) y = −x³ + 3x

- Tạo các thanh trượt biểu thị các tham số a, b, c, d bằng cách nhấp chuột liên tiếp vào thanh công cụ và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

- Nhập hàm số y = −x³ + 3x vào vùng nhập lệnh.

- Ta được đồ thị như hình vẽ

Nhận xét:

Hàm số nghịch biến trên các khoảng (−∞; −1) và (1; +∞).

Hàm số đồng biến trên khoảng (−1; 1).

Điểm cực đại là (1; 2), điểm cực tiểu là (−1; −2).

Đồ thị hàm số có tâm đối xứng là (0; 0).

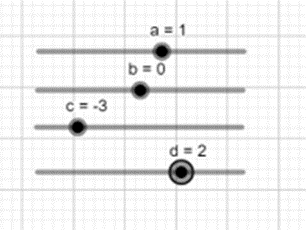
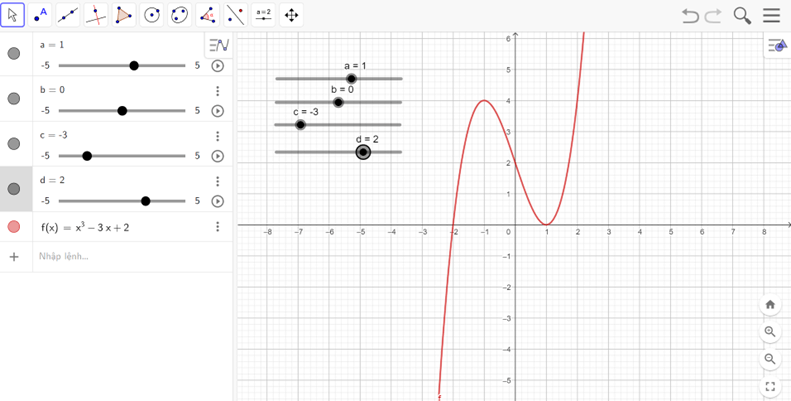
d) y = x³ – 3x + 2

- Tạo các thanh trượt biểu thị các tham số a, b, c, d bằng cách nhấp chuột liên tiếp vào thanh công cụ và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

- Nhập hàm số y = x³ – 3x + 2 vào vùng nhập lệnh.

- Ta được đồ thị như hình vẽ

Nhận xét:

Hàm số đồng biến trên các khoảng (−∞; −1) và (1; +∞).

Hàm số nghịch biến trên khoảng (−1; 1).

Điểm cực đại là (−1; 4), điểm cực tiểu là (1; 0).

Đồ thị hàm số có tâm đối xứng là (0; 2).

Thực hành 2 trang 89 Toán 12 Tập 1: Vẽ đồ thị các hàm số sau:

a) y = $\frac{x+1}{x-1}$ ;       b) y = $\frac{-x-1}{x-1}$ .

Lời giải:

a) y = $\frac{x+1}{x-1}$

- Tạo các thanh trượt biểu thị các tham số a, b, c, d

- Nhập hàm số y = $\frac{x+1}{x-1}$ vào ô lệnh.

- Nhập phương trình hai đường tiệm cận x = 1; y = 1.

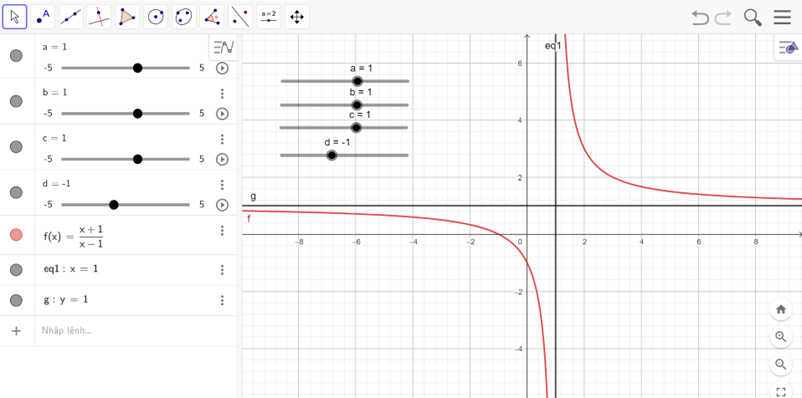
- Ta được đồ thị như hình vẽ

Nhận xét

Hàm số nghịch biến trên khoảng (−∞; 1) và (1; +∞).

Hàm số không có cực trị.

Đồ thị hàm số nhận x = 1 là tiệm cận đứng và y = 1 là tiệm cận ngang.

Tâm đối xứng của đồ thị hàm số là (1; 1).

b) y = $\frac{-x-1}{x-1}$

- Tạo các thanh trượt biểu thị các tham số a, b, c, d

- Nhập hàm số y = $\frac{-x-1}{x-1}$ vào ô lệnh.

- Nhập phương trình hai đường tiệm cận x = 1; y = −1.

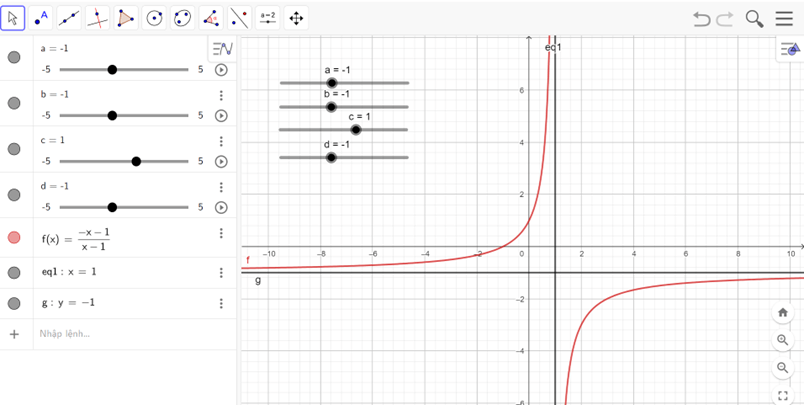
- Ta được đồ thị như hình vẽ

Nhận xét

Hàm số đồng biến trên khoảng (−∞; 1) và (1; +∞).

Hàm số không có cực trị.

Đồ thị hàm số nhận x = 1 là tiệm cận đứng và y = −1 là tiệm cận ngang.

Tâm đối xứng của đồ thị hàm số là (1; −1).