Bài 1.40 trang 43 Toán 12 Tập 1 - Kết nối tri thức

Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:

Giải Toán 12 Bài tập cuối chương 1 - Kết nối tri thức

Bài 1.40 trang 43 Toán 12 Tập 1: Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:

a) y = x³ – 3x² + 3x – 1; b) y = x⁴ – 2x² – 1;

c) $y = \frac{2 x - 1}{3 x + 1}$ ; d) $y = \frac{x^{2} + 2 x + 2}{x + 1}$ .

Lời giải:

a) y = x³ – 3x² + 3x – 1

Tập xác định của hàm số là ℝ.

Có y' = 3x² – 6x + 3; y' = 0 ⇔ 3x² – 6x + 3 = 0 ⇔ x = 1.

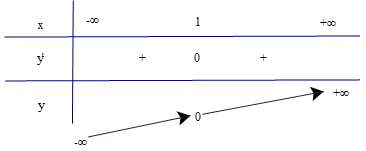
Bảng biến thiên

Bài 1.40 trang 43 Toán 12 Tập 1 | Kết nối tri thức Giải Toán 12

Hàm số đồng biến trên các khoảng (−∞; 1) và (1; +∞).

Hàm số không có cực trị.

b) y = x⁴ – 2x² – 1

Tập xác định: D = ℝ.

Có y' = 4x³ – 4x; y' = 0 ⇔ 4x³ – 4x = 0 ⇔ x = 0 hoặc x = 1 hoặc x = −1.

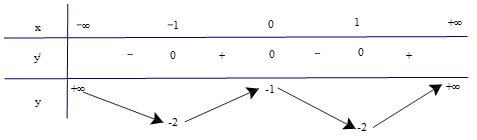
Bảng biến thiên

Bài 1.40 trang 43 Toán 12 Tập 1 | Kết nối tri thức Giải Toán 12

Hàm số đồng biến trên các khoảng (−1; 0) và (1; +∞).

Hàm số nghịch biến trên các khoảng (−∞; −1) và (0; 1).

Hàm số đạt cực đại tại x = 0 và y_CĐ = −1.

Hàm số đạt cực tiểu tại x = −1; x = 1 và y_CT = −2.

c) $y = \frac{2 x - 1}{3 x + 1}$

Tập xác định: $D = ℝ \ \{\frac{- 1}{3}\}$

Có $y^{'} = \frac{2 (3 x + 1) - 3 (2 x - 1)}{{(3 x + 1)}^{2}} = \frac{5}{{(3 x + 1)}^{2}} > 0, \forall x \neq - \frac{1}{3}$

Hàm số đồng biến trên các khoảng $(- \infty; - \frac{1}{3})$ và $(- \frac{1}{3}; + \infty)$ .

Hàm số không có cực trị.

d) $y = \frac{x^{2} + 2 x + 2}{x + 1}$

Tập xác định: D = ℝ\{−1}.

Có $y^{'} = \frac{(2 x + 2) (x + 1) - (x^{2} + 2 x + 2)}{{(x + 1)}^{2}} = \frac{x^{2} + 2 x}{{(x + 1)}^{2}}$

Có y' = 0 ⇔ x² + 2x = 0 ⇔ x = 0 hoặc x = −2.

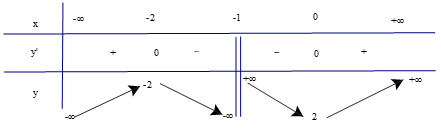
Bảng biến thiên

Bài 1.40 trang 43 Toán 12 Tập 1 | Kết nối tri thức Giải Toán 12

Hàm số đồng biến trên các khoảng (−∞; −2) và (0; +∞).

Hàm số nghịch biến trên các khoảng (−2; −1) và (−1; 0).

Hàm số đạt cực đại tại x = −2 và y_CĐ = −2.

Hàm số đạt cực tiểu tại x = 0 và y_CT = 2.

Lời giải bài tập Toán 12 Bài tập cuối chương 1 hay, chi tiết khác: