Giải Toán 12 trang 79 Tập 1 Kết nối tri thức

---

Với Giải Toán 12 trang 79 Tập 1 trong Bài 9: Khoảng biến thiên và khoảng tứ phân vị Toán 12 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 79.

Giải Toán 12 trang 79 Tập 1 Kết nối tri thức

Bài 3.2 trang 79 Toán 12 Tập 1: Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:

Tính mức thu nhập trung bình của người lao động ở hai nhà máy trên. Dựa vào khoảng tứ phân vị, hãy xác định xem mức thu nhập của người lao động ở nhà máy nào biến động nhiều hơn.

Lời giải:

Chọn giá trị đại diện cho mẫu số liệu ta có:

Mức thu nhập trung bình của người lao động nhà máy A là:

$\frac{\mathrm{6,5.20}+\mathrm{9,5.35}+\mathrm{12,5.45}+\mathrm{15,5.35}+\mathrm{18,5.20}}{\left(20+35+45+35+20\right)}=\mathrm{12,5}$(triệu đồng).

Mức thu nhập trung bình của người lao động nhà máy B là:

$\frac{\mathrm{6,5.17}+\mathrm{9,5.23}+\mathrm{12,5.30}+\mathrm{15,5.23}+\mathrm{18,5.17}}{\left(17+23+30+23+17\right)}=\mathrm{12,5}$ (triệu đồng).

Nhà máy A

Cỡ mẫu n = 20 + 35 + 45 + 35 + 20 = 155.

Gọi x₁; x₂; …; x₁₅₅ là mức thu nhập của 155 công nhân lao động của nhà máy A và được sắp xếp theo thứ tự tăng dần

Tứ phân vị thứ nhất của mẫu số liệu là x₃₉ thuộc nhóm [8; 11) nên nhóm chứa tứ phân vị thứ nhất là [8; 11).

Ta có $Q_1=8+\frac{\frac{155}{4}-20}{35}.\left(11-8\right)\approx \mathrm{9,6}$.

Tứ phân vị thứ ba của mẫu số liệu là x₁₁₇ thuộc nhóm [14; 17) nên nhóm chứa tứ phân vị thứ ba là [14; 17).

Ta có $Q_3=14+\frac{\frac{155.3}{4}-100}{35}.\left(17-14\right)\approx \mathrm{15,4}$ .

Khoảng tứ phân vị: R_AQ = 15,4 – 9,6 = 5,8.

Nhà máy B

Cỡ mẫu n = 17 + 23 + 30 + 23 + 17 = 110.

Gọi y₁; y₂; …; y₁₁₀ là mức thu nhập của 110 công nhân lao động của nhà máy B và được sắp xếp theo thứ tự tăng dần.

Tứ phân vị thứ nhất của mẫu số liệu là y₂₈ thuộc nhóm [8; 11) nên nhóm chứa tứ phân vị thứ nhất là [8; 11).

Ta có $Q_1=8+\frac{\frac{110}{4}-17}{23}.\left(11-8\right)\approx \mathrm{9,4}$.

Tứ phân vị thứ ba của mẫu số liệu là y₈₃ thuộc nhóm [14; 17) nên nhóm chứa tứ phân vị thứ ba là [14; 17).

Ta có $Q_3=14+\frac{\frac{3.110}{4}-70}{23}.\left(17-14\right)\approx \mathrm{15,6}$ .

Khoảng tứ phân vị .

Vì R_BQ > R_AQ nên mức thu nhập của người lao động ở nhà máy B biến động nhiều hơn.

Bài 3.3 trang 78 Toán 12 Tập 1: Bảng sau đây cho biết chiều cao của các học sinh lớp 12A và 12B.

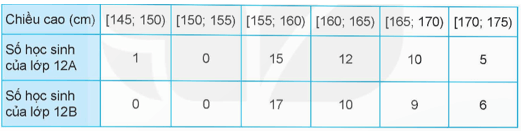
a) Tìm khoảng biến thiên, khoảng tứ phân vị cho các mẫu số liệu ghép nhóm về chiều cao của học sinh lớp 12A, 12B.

b) Để so sánh độ phân tán về chiều cao của học sinh hai lớp này ta nên dùng khoảng biến thiên hay khoảng tứ phân vị? Vì sao?

Lời giải:

Lớp 12A

+) Khoảng biến thiên: R₁ = 175 – 145 = 30.

+) Cỡ mẫu n = 1 + 0 + 15 + 12 + 10 + 5 = 43.

Gọi x₁; x₂; …; x₄₃ là chiều cao của 43 học sinh lớp 12A được sắp xếp theo thứ tự tăng dần.

Tứ phân vị thứ nhất của mẫu số liệu là x₁₁ thuộc nhóm [155; 160) nên nhóm chứa tứ phân vị thứ nhất là [155; 160).

Ta có $Q_1=155+\frac{\frac{43}{4}-1}{15}.\left(160-155\right)=\mathrm{158,25}$ .

Tứ phân vị thứ ba của mẫu số liệu là x₃₃ thuộc nhóm [165; 170) nên nhóm chứa tứ phân vị thứ ba là [165; 170).

Ta có $Q_3=165+\frac{\frac{43.3}{4}-28}{10}.\left(170-165\right)=\mathrm{167,125}$ .

Khoảng tứ phân vị là D_1Q = 167,125 – 158,25 = 8,875.

Lớp 12B

+) Khoảng biến thiên: R₂ = 175 – 155 = 20.

+) Cỡ mẫu n = 17 + 10 + 9 + 6 = 42.

Gọi y₁; y₂; …; y₄₂ là chiều cao của 42 học sinh lớp 12B và được sắp xếp theo thứ tự tăng dần.

Tứ phân vị thứ nhất của mẫu số liệu là y₁₁ thuộc nhóm [155; 160) nên nhóm chứa tứ phân vị thứ nhất là [155; 160).

Ta có $Q_1=155+\frac{\frac{42}{4}-0}{17}.\left(160-155\right)\approx \mathrm{158,1}$.

Tứ phân vị thứ ba của mẫu số liệu là y₃₂ thuộc nhóm [165; 170) nên nhóm chứa tứ phân vị thứ ba là [165; 170).

Ta có $Q_2=165+\frac{\frac{42.3}{4}-27}{9}.\left(170-165\right)=\mathrm{167,5}$ .

Khoảng tứ phân vị là: R_2Q = 167,5 – 158,1 = 9,4.

b) Để so sánh độ phân tán về chiều cao của học sinh hai lớp này, ta nên dùng khoảng tứ phân vị vì khoảng tứ phân vị chỉ phụ thuộc vào nửa giữa của mẫu số liệu, không bị ảnh hưởng bởi các giá trị bất thường.

Lời giải bài tập Toán 12 Bài 9: Khoảng biến thiên và khoảng tứ phân vị hay khác:

• Giải Toán 12 trang 76

• Giải Toán 12 trang 77

• Giải Toán 12 trang 78