10 Bài tập Trắc nghiệm Tính đơn điệu và cực trị của hàm số (có đáp án) - Kết nối tri thức Toán 12

---

Haylamdo biên soạn và sưu tầm với 10 bài tập trắc nghiệm Tính đơn điệu và cực trị của hàm số Toán 12 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh lớp 12 ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 12.

10 Bài tập Trắc nghiệm Tính đơn điệu và cực trị của hàm số (có đáp án) - Kết nối tri thức Toán 12

I. Nhận biết

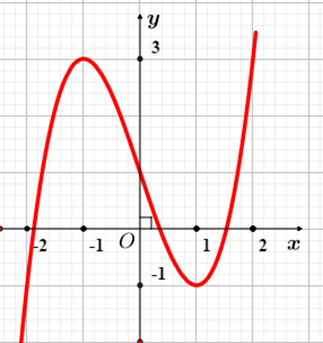
Câu 1. Cho hàm số $y=f\left(x\right)$ có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào?

A. $\left(-2;2\right)$.

B.$\left(0;2\right)$ .

C.$\left(-1;1\right)$ .

D.$\left(1;2\right)$ .

Hiển thị đáp án

Đáp án đúng là: D

- Xét đáp án A, trên khoảng $\left(-2;2\right)$ đồ thị có đoạn hướng đi lên là hàm số đồng biến và có đoạn hướng đi xuống là hàm số nghịch biến nên loại.

- Xét đáp án B, trên khoảng $\left(0;2\right)$ đồ thị có đoạn hướng đi xuống là hàm số nghịch biến và có đoạn hướng đi lên là hàm số đồng biến nên loại.

- Xét đáp án C, trên khoảng $\left(-1;1\right)$ đồ thị có hướng đi xuống là hàm số nghịch biến nên loại.

- Xét đáp án D, trên khoảng $\left(1;2\right)$ đồ thị có hướng đi lên là hàm số đồng biến nên chọn.

Câu 2. Cho hàm số $y=f\left(x\right)$ có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

.

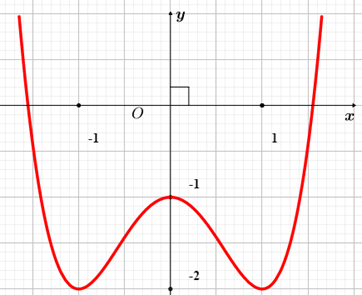
A. (0; 1).

B. (−∞; 1).

C. (−1; 1).

D. (−1; 0).

Hiển thị đáp án

Đáp án đúng là: D

Quan sát đồ thị ta thấy đồ thị đi lên trong các khoảng $(-1;0)$và $(1;+\infty ).$

Vậy hàm số đồng biến trên các khoảng $(-1;0)$ và $(1;+\infty ).$

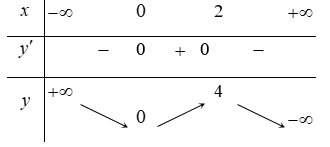
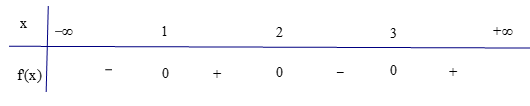
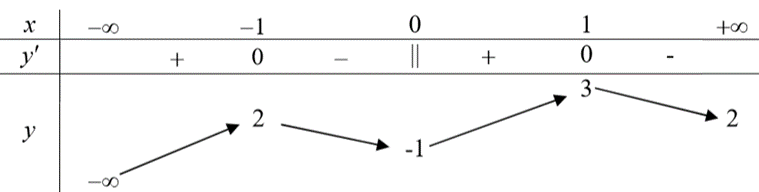
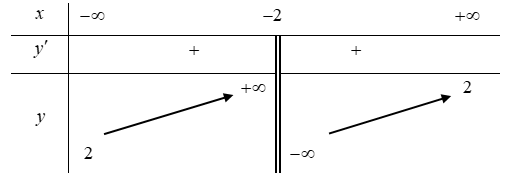
Câu 3. Cho hàm số $y=f\left(x\right)$ có bảng biến thiên như hình vẽ sau

Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng $\left(-1;3\right)$.

B. Hàm số đồng biến trên khoảng $\left(-\infty ;2\right)$.

C. Hàm số nghịch biến trên khoảng $\left(-2;1\right)$.

D. Hàm số nghịch biến trên khoảng $\left(1;2\right)$.

Hiển thị đáp án

Đáp án đúng là: D

Dựa vào bảng biến thiên ta có hàm số nghịch biến trên khoảng $\left(1;2\right)$.

Câu 4. Cho hàm số $y=f\left(x\right)$ xác định, liên tục trên $\mathrm{ℝ}$ và có đồ thị là đường cong như hình vẽ. Hàm số đạt cực đại tại điểm nào dưới đây?

A. $x=-3$.

B. $x=1$.

C.$x=0$ .

D.$x=2$ .

Hiển thị đáp án

Đáp án đúng là: C

Từ đồ thị hàm số ta có hàm số đạt cực đại tại $x=0$.

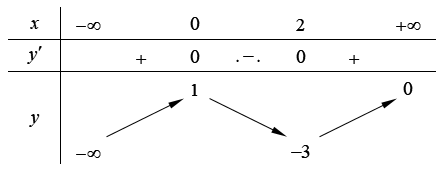
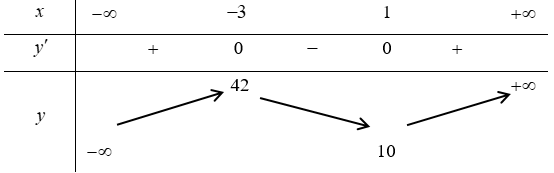
Câu 5. Cho hàm số $y=f\left(x\right)$liên tục trên $ℝ$và có bảng biến thiên như sau

Giá trị cực đại của hàm số $y=f\left(x\right)$ bằng

A. $x=0$.

B.$x=2$ .

C.$y=-3$ .

D. $y=1$.

Hiển thị đáp án

Đáp án đúng là: D

Dựa vào bảng biến thiên ta có hàm số đạt cực đại tại x = 0 và giá trị cực đại là $y=1$.

II. Thông hiểu

Câu 6. Cho hàm số $y=x^3+3x^2-9x+15$. Khẳng định nào sau đây là khẳng định sai?

A. Hàm số nghịch biến trên khoảng (-3;1).

B. Hàm số đồng biến trên (-9;-5).

C. Hàm số đồng biến trên $ℝ$ .

D. Hàm số đồng biến trên $\left(5;+\infty \right)$.

Hiển thị đáp án

Đáp án đúng là: C

Tập xác định: $D=ℝ$

Ta có $y^{\text{'}}=3x^2+6x-9$ ;$y^{\text{'}}=0\iff \left(\begin{array}{c}x=1\\ x=-3\end{array}\right)$.

Bảng biến thiên:

Kết luận: Hàm số đồng biến trên các khoảng: $\left(-\infty ;-3\right),\left(1;+\infty \right)$.

Hàm số nghịch biến trên khoảng (-3;1).

Câu 7.Chọn mệnh đề đúng về hàm số $y=\frac{2x-1}{x+2}$ .

A. Hàm số nghịch biến trên từng khoảng xác định của nó.

B. Hàm số đồng biến trên tập xác định của nó.

C. Hàm số đồng biến trên từng khoảng xác định của nó.

D. Hàm số nghịch biến trên tập xác định của nó.

Hiển thị đáp án

Đáp án đúng là: C

Tập xác định:$D=ℝ\backslash \left(-2\right)$ .

Ta có: $y^{\text{'}}=\frac{5}{{\left(x+2\right)}^2}>0,\forall x\ne -2$. Nên hàm số đồng biến trên từng khoảng xác định của nó.

Bảng biến thiên:

Câu 8. Hàm số nghịch biến khi $y=-x^3+3x^2+1$ thuộc khoảng nào sau đây?

A. (0;2)                                                                              

B.$(0;+\infty ).$

C. $(-\infty ;2).$                                                                           

D. $(-\infty ;0)$ và $(2;+\infty ).$

Hiển thị đáp án

Đáp án đúng là: D

Ta có:$y^{\text{'}}=-3x^2+6x<0\iff x\in \left(-\infty ;0\right)\cup \left(2;+\infty \right)$.

Câu 9. Cho hàm số $y=x^2\left(3-x\right)$. Mệnh đề nào sau đây là đúng?

A. Hàm số đã cho đồng biến trên khoảng $\left(-\infty ;0\right)$.

B. Hàm số đã cho đồng biến trên khoảng $\left(2;+\infty \right)$.

C. Hàm số đã cho đồng biến trên khoảng (0;2).

D. Hàm số đã cho đồng biến trên khoảng $\left(-\infty ;3\right)$.

Hiển thị đáp án

Đáp án đúng là: C

Ta có $y=-x^3+3x^2$;$y^{\text{'}}=-3x^2+6x$ ;

.

Bảng biến thiên:

Vậy hàm số đã cho đồng biến trên (0;2).

III. Vận dụng

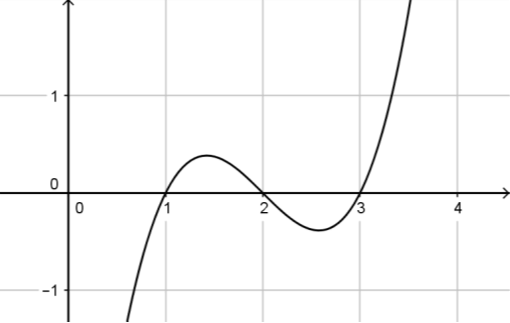
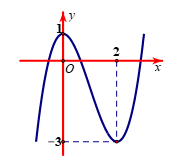
Câu 10. Cho hàm số $y=f\left(x\right)$. Hàm số $y=f\text{'}\left(x\right)$ có đồ thị như hình vẽ:

Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số $y=f\left(x\right)$ cắt trục hoành tại ba điểm phân biệt.

B. Đồ thị hàm số $y=f\left(x\right)$ có hai điểm cực trị.

C. Đồ thị hàm số $y=f\left(x\right)$ có ba điểm cực trị.

D. Đồ thị hàm số $y=f\left(x\right)$ có một điểm có một điểm cực trị.

Hiển thị đáp án

Đáp án đúng là: C

Dựa vào đồ thị hàm số ta có bảng xét dấu sau

Hàm số đạt cực trị tại x = 1; x = 2; x = 3.

Vậy đồ thị hàm số có ba điểm cực trị.
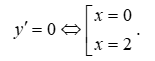