Giải Toán lớp 6 trang 59 Tập 1 Cánh diều
Haylamdo biên soạn và sưu tầm với giải Toán lớp 6 trang 59 Tập 1 trong Bài tập cuối chương 1 Toán lớp 6 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán lớp 6 trang 59.
Giải Toán lớp 6 trang 59 Tập 1 Cánh diều
Bài 1 trang 59 Toán lớp 6 Tập 1: Thực hiện các phép tính sau:
a) 4 . 25 – 12 . 5 + 170 : 10;
b) (7 + 33 : 32) . 4 – 3;
c) 12 : {400 : [500 – (125 + 25 . 7)]};
d) 168 + {[2 . (24 + 32) – 2560] : 72}.
Lời giải:
a) 4 . 25 – 12 . 5 + 170 : 10
= 100 – 60 + 17
= 40 + 17
= 57.
b) (7 + 33 : 32) . 4 – 3
= (7 + 33 – 2) . 4 – 3
= (7 + 31) . 4 – 3
= (7 + 3) . 4 – 3
= 10 . 4 – 3
= 40 – 3 = 37.
c) 12 : {400 : [500 – (125 + 25 . 7)]}
= 12 : {400 : [500 – (125 + 175)]}
= 12 : [400 : (500 – 300)]
= 12 : (400 : 200)
= 12 : 2
= 6.
d) 168 + {[2 . (24 + 32) – 2560] : 72}
= 168 + {[2 . (16 + 9) – 1] : 49}
= 168 + [(2. 25 – 1) : 49]
= 168 + [(50 – 1) : 49]
= 168 + (49 : 49)
= 168 + 1 = 169.
Bài 2 trang 59 Toán lớp 6 Tập 1: Gọi P là tập hợp các số nguyên tố. Chọn kí hiệu "∈", "∉" thích hợp cho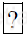 
:
a) 2 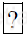P;
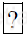b) 47 P;
c) a 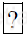P với a = 3 . 5 . 7 . 9 + 20;
d) b 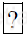P với b = 5 . 7 . 11 + 13 . 17.
Lời giải:
Ta có: P là tập hợp các số nguyên tố.
a) Vì 2 chỉ có hai ước là 1 và chính nó nên 2 là số nguyên tố hay 2 thuộc P.
Do đó 2 
P.
b) Vì 47 chỉ có hai ước là 1 và 47, nên 47 là số nguyên tố hay 47 thuộc P.
Do đó 47 P.
c) Ta có: a = 3 . 5 . 7 . 9 + 20 = 15 . 7 . 9 + 20 = 105 . 9 + 20 = 945 + 20 = 965
Vì 965 : 5 = 193 nên số 965 ngoài có hai ước là 1 và 965, còn có thêm ít nhất một ước nữa là 5 nên 965 hay a là hợp số.
Do đó a không phải là số nguyên tố nên a không thuộc P.
Vậy a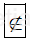 
P.
d) Ta có: b = 5 . 7 . 11 + 13 . 17 = 35 . 11 + 221 = 385 + 221 = 606
Vì 606 : 6 = 101 nên số 606 ngoài có hai ước là 1 và 606, còn có thêm ít nhất một ước nữa là 6 nên 606 là hợp số hay b là hợp số.
Do đó b không phải là số nguyên tố nên b không thuộc P.
Vậy b 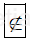P.
Bài 3 trang 59 Toán lớp 6 Tập 1: Phân tích các số sau ra thừa số nguyên tố:
a) 51;
b) 76;
c) 225;
d) 1 800.
Lời giải:
Ta có thể phân tích một số ra thừa số nguyên tố bằng cách viết "theo cột dọc" hoặc "rẽ nhánh".
a) Ta có:
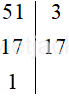
Vậy 51 = 3 . 17.
b) Ta có:
Vậy 76 = 2 . 2 . 19 = 22 . 19.
c) Ta có:
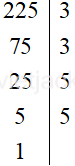
Vậy 225 = 3 . 3 . 5 . 5 = 32 . 52.
d) Ta có: 1 800 = 10 . 180
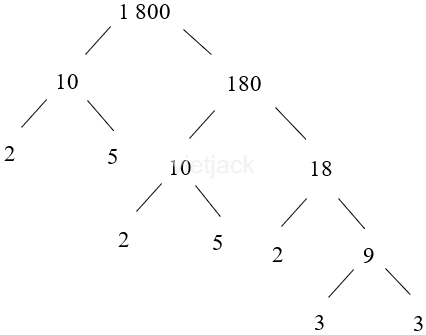
Vậy 1 800 = 2 . 5 . 2 . 5 . 2 . 3 . 3 = 23 . 32 . 52.
Bài 4 trang 59 Toán lớp 6 Tập 1: Tìm ƯCLN của hai số:
a) 40 và 60;
b) 16 và 124;
c) 41 và 47.
Lời giải:
a) 40 và 60
Ta có:
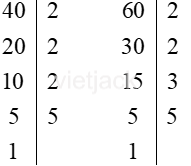
Do đó: 40 = 2 . 2 . 2 . 5 = 23 . 5
60 = 2 . 2 . 3 . 5 = 22 . 3 . 5
Các thừa số nguyên tố chung của 40 và 60 là 2 và 5
Số 2 có số mũ nhỏ nhất là 2; số 5 có số mũ nhỏ nhất là 1
Vậy ƯCLN(40, 60) = 22 . 51 = 4 . 5 = 20.
b) 16 và 124
Ta có: 16 = 24
Lại có
Do đó: 124 = 2 . 2 . 31 = 22 . 31
Thừa số nguyên tố chung của 16 và 124 là 2, với số mũ nhỏ nhất là 2.
Vậy ƯCLN(16, 124) = 22 = 4.
c) 41 và 47
Ta có: số 41 chỉ có hai ước là 1 và 41 nên 41 là số nguyên tố
Số 47 chỉ có hai ước là 1 và 47 nên 47 cũng là số nguyên tố
Do đó 41 và 47 là hai số nguyên tố cùng nhau.
Vậy ƯCLN(41, 47) = 1.
Bài 5 trang 59 Toán lớp 6 Tập 1: Tìm BCNN của các số sau
a) 72 và 540.
b) 28, 49, 64.
c) 43 và 53.
Lời giải:
a) 72 và 540
Ta có:
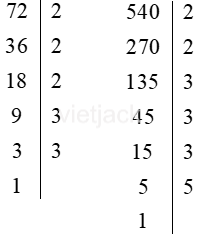
Do đó: 72 = 2 . 2 . 2 . 3 . 3 = 23 . 32
540 = 2 . 2 . 3 . 3 . 3 . 5 = 22 . 33 . 5
Các thừa số nguyên tố chung và riêng của 72 và 540 là 2, 3, 5
Số hai có số mũ lớn nhất là 3; số 3 có số mũ lớn nhất là 3; số 5 có số mũ lớn nhất là 1.
Vậy BCNN(72, 540) = 23 . 33 . 51 = 8 . 27 . 5 = 1 080.
b) 28, 49, 64
Ta có: 28 = 4 . 7 = 22 . 7
49 = 72; 64 = 26
Các thừa số nguyên tố chung và riêng của 28, 49 và 64 là 2, 7
Số 2 có số mũ lớn nhất là 6, số 7 có số mũ lớn nhất là 2.
Vậy BCNN(28, 49, 64) = 26 . 72 = 64 . 49 = 3 136.
c) 43 và 53
Ta có: 43 chỉ có hai ước là 1 và 43 nên 43 là số nguyên tố
53 chỉ có hai ước là 1 và 53 nên nó cũng là số nguyên tố
Do đó 43 và 53 là hai số nguyên tố cùng nhau.
Vậy BCNN(43, 53) = 43 . 53 = 2 279.
Bài 6 trang 59 Toán lớp 6 Tập 1: Dọc theo hai bên của một con đường dài 1 500m, các cột điện được dựng cách nhau 75 m (bắt đầu dựng từ đầu đường). Để tăng cường ánh sáng, người ta dựng lại các cột điện ở cả hai bên con đường (cũng bắt đầu dựng từ đầu đường) sao cho ở mỗi bên đường các cột điện chỉ còn cách nhau 50m. Họ tận dụng những cột điện cũ không phải dời đi. Hãy tính tổng chi phí cần thiết để hoàn thành dựng cột điện mới cho con đường, biết chi phí dựng một cột điện mới là 4 triệu đồng.
Lời giải:
Người ta dựng cột điện dọc theo hai bên của một con đường nên ta tính số cột điện cần phải dựng thêm mới trong một bên trước, sau đó nhân đôi lên, ta được tổng tất cả số cột điện mới cần dựng trên cả con đường.
Do số cột điện cũ dựng ở một bên đường được bắt đầu dựng từ đầu đường tới hết con đường và các cột điện được dựng cách nhau 75 m nên vị trí dựng các cột điện này là bội của 75 và không quá 1500.
Mà các bội của 75 và không quá 1500 là: 0; 75; 150; 225; 300; 375; 450; 525; 600; 675; 750; 825; 900; 975; 1050; 1125; 1200; 1275; 1350; 1425; 1500.
Do đó ta có 21 cột điện cũ được dựng một bên đường (thứ tự từ cột 1 đến cột 21 tương ứng với các vị trí đặt cột từ vị trí 0 m đến 1500 m).
Để tăng cường ánh sáng, người ta dựng lại các cột điện cũng bắt đầu từ đầu đường, cách nhau 50 m và tận dụng lại các cột cũ không phải dời đi, có nghĩa các vị trí cột cũ không phải dời đi là các bội chung của 50; 75 và không quá 1500.
Ta có: 50 = 2 . 25 = 2 . 52; 75 = 3 . 25 = 3 . 52
Suy ra BCNN(50, 75) = 2 . 3 . 52 = 150.
Do đó ta có các bội chung của 50; 75 và không quá 1500 là bội của BCNN(50,75) = 150 và không quá 1500, đó là: 0; 150; 300; 450; 600; 750; 900; 1050; 1200; 1350; 1500.
Nên ta có 11 cột cũ được giữ lại tận dụng, tương ứng với thứ tự các cột điện cũ ở một bên là cột 1; 3; 5; 7; 9; 11; 13; 15; 17; 19; 21.
Mà khoảng cách giữa các cột cũ là đều nhau và bằng 150 m và có 10 khoảng cách cần dựng thêm cột điện mới.
Cho nên ta cần dựng thêm 2 cột điện mới ở vị trí cộng thêm 50 m và 100 m trong từng khoảng cách giữa hai cột cũ được giữ lại.
Do đó, ở một bên đường, ta cần dựng thêm: 2 . 10 = 20 (cột điện mới)
Suy ra ở cả hai bên đường, ta cần dựng thêm số cột điện mới là:
20 . 2 = 40 (cột điện mới)
Tổng chi phí cần thiết để hoàn thành dựng cột điện mới cho con đường là:
4 000 000 . 40 = 160 000 000 (đồng)
Vậy tổng chi phí cần thiết để hoàn thành dựng cột điện mới cho con đường là 160 triệu đồng.
Bài 7 trang 59, 60 Toán lớp 6 Tập 1: Hệ Mặt Trời gồm tám hành tinh, đó là: Sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương. Các hành tinh trong Hệ Mặt Trời chia thành hai nhóm. Nhóm trong gồm: Sao Thủy, Sao Kim, Trái Đất, Sao Hỏa. Nhóm ngoài gồm: Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương. Các hành tinh nhóm trong có khối lượng và kích thước khá nhỏ so với các hành tinh nhóm ngoài. Hai nhóm hành tinh ngăn cách nhau bởi một vành đại tiểu hành tinh và vô số các thiên thạch nhỏ cùng quay quanh Mặt Trời.
a) Viết tập hợp A gồm tám hành tinh trong hệ Mặt Trời.
b) Sắp xếp kích thước của tám hành tinh trong hệ Mặt Trời theo thứ tự tăng dần.
c) Viết tập hợp B gồm bốn hành tinh có kích thước nhỏ nhất và tập hợp C gồm bốn hành tinh có kích thước lớn nhất.
Lời giải:
a) Tám hành tinh trong hệ Mặt Trời là: Sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương.
Do đó ta viết tập hợp A là:
A = {Sao Thủy; Sao Kim; Trái Đất; Sao Hỏa; Sao Mộc; Sao Thổ; Sao Thiên Vương; Sao Hải Vương}.
b) Quan sát bảng kích thước của các hành tinh:
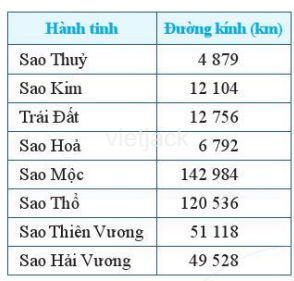
Vì 4 879 < 6 792 < 12 104 < 12 756 < 49 528 < 51 118 < 120 536 < 142 984.
Khi đó ta có sắp xếp kích thước của các hành tinh tương ứng là:
Sao Thuỷ < Sao Hỏa < Sao Kim < Trái Đất < Sao Hải Vương < Sao Thiên Vương < Sao Thổ < Sao Mộc.
Vậy kích thước của các hành tinh trong hệ Mặt Trời được sắp xếp theo thứ tự tăng dần như sau: Sao Thuỷ; Sao Hỏa; Sao Kim; Trái Đất; Sao Hải Vương; Sao Thiên Vương; Sao Thổ; Sao Mộc.
c)
+ Bốn hành tinh có kích thước nhỏ là: Sao Thủy, Sao Hỏa, Sao Kim, Trái Đất.
Nên ta viết tập hợp B là:
B = {Sao Thủy; Sao Hỏa; Sao Kim; Trái Đất}
+ Bốn hành tinh có kích thước lớn là: Sao Hải Vương, Sao Thiên Vương, Sao Thổ, Sao Mộc.
Nên ta viết tập hợp C là:
C = {Sao Hải Vương; Sao Thiên Vương; Sao Thổ; Sao Mộc}.
